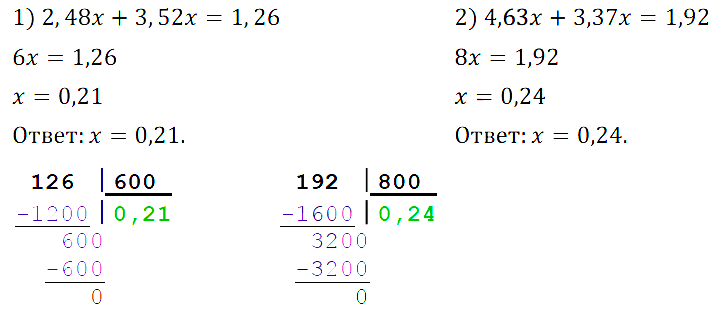Упражнения по математике для УМК Мерзляк с ответами на некоторые задачи. §1. Делители и кратные (2019, 2020, 2021 годы). Математика 6 Мерзляк. Упражнения 01-39.
ОГЛАВЛЕНИЕ (2021 год) ТЕОРИЯ: § 1.
Математика 6 Мерзляк. Упражнения 01-39
№ 1. Верно ли утверждение: 1) число 6 является делителем числа 24; 2) число 6 кратно числу 24; 3) число 5 является делителем числа 51; 4) число 9 является делителем числа 99; 5) число 18 кратно числу 3; 6) число 28 кратно числу 8?
Правильный ответ: 1) число 6 является делителем числа 24 — верно;
2) число 6 кратно числу 24 — НЕверно;
3) число 5 является делителем числа 51 — НЕверно;
4) число 9 является делителем числа 99 — верно;
5) число 18 кратно числу 3 — верно;
6) число 28 кратно числу 8 — НЕверно.
№ 2. Какие из чисел 2, 3, 4, 6, 8, 9, 10, 12, 15, 16, 18, 30 являются: 1) делителями 24; 2) кратными 6; 3) делителями 20 и 24; 4) делителями 24 и кратными 4?
Правильный ответ: 1) делителями 24: 2, 3, 4, 6, 8, 12;
2) кратными 6: 6, 12, 18, 30;
3) делителями 20 и 24: 2, 4;
4) делителями 24 и кратными 4: 4, 8, 12.
№ 3. Чему равняется: 1) наибольший делитель числа 19 735; 2) наименьший делитель числа 19 735; 3) наименьшее кратное числа 19 735?
Правильный ответ: 1) наибольший делитель числа 19 735: 19 735.
2) наименьший делитель числа 19 735: 1;
3) наименьшее кратное числа 19 735: 19 735.
№ 4. Запишите все делители числа: 1) 18; 2) 8; 3) 13; 4) 56.
Правильный ответ: 1) делители числа 18: 1, 2, 3, 6, 9, 18;
2) делители числа 8: 1, 2, 4, 8;
3) делители числа 13: 1, 13;
4) делители числа 56: 1, 2, 4, 7, 8, 14, 28, 56.
№ 5. Запишите все делители числа: 1) 30; 2) 12; 3) 23; 4) 72.
Правильный ответ: 1) делители числа 30: 1, 2, 3, 5, 6, 10, 15, 30;
2) делители числа 12: 1, 2, 3, 4, 6, 12;
3) делители числа 23: 1, 23;
4) делители числа 72: 1, 2, 3, 4, б, 8, 9, 12, 18, 24, 36, 72.
№ 6. Запишите пять чисел, кратных числу: 1) 7; 2) 30; 3) 100; 4) 34.
Правильный ответ: 1) кратных числу 7: 7, 14, 21, 28, 35;
2) кратных числу 30: 30, 60, 90, 120, 150;
3) кратных числу 100: 100, 200, 300, 400, 500;
4) кратных числу 34: 34, 68, 102, 136, 170.
№ 7. Запишите четыре числа, кратных числу: 1) 16; 2) 12; 3) 150; 4) 47.
Правильный ответ: 1) кратных числу 16: 16, 32, 48, 64;
2) кратных числу 12: 12, 24, 36, 48;
3) кратных числу 150: 150, 300, 450, 600;
4) кратных числу 47: 47, 94, 141, 188.
№ 8. Из чисел 28, 36, 48, 64, 92, 100, 108, 110 выпишите те, которые: 1) кратны 4; 2) не кратны 6.
Правильный ответ: 1) кратны 4: 28, 36, 48, 64, 92, 100, 108;
2) не кратны 6: 28, 64, 92, 100, 110.
№ 9. Известно, что сумма натуральных чисел а и b делится нацело на 5. Верно ли, что: 1) каждое из чисел а и b делится нацело на 5; 2) одно из чисел делится нацело на 5, а другое – нет? Ответ проиллюстрируйте примерами.
Правильный ответ: 1) Неверно. Если сумма натуральных чисел а и b делится нацело на 5, то необязательно каждое из чисел а и b делится на 5.
Например, а = 7; b = 3 (не делятся на 5): а + b = 7 + 3 = 10 – делится на 5.
2) Неверно. Если сумма натуральных чисел а и b делится нацело на 5, а одно из чисел делится нацело на 5, то и другое число должно делиться на 5.
Например, а = 10; b = 15 (делятся на 5): а + b = 10 + 15 = 25 – делится нацело на 5.
№ 10. Известно, что каждое из чисел а и b не делится нацело на 3. Верно ли, что их сумма также не делится нацело на 3?
Правильный ответ: Неверно, так как если каждое из чисел а и b не делятся нацело на 3, то их сумма может делиться на 3. Например, а = 5; b = 7 (не делятся нацело на 3): а + b = 5 + 7 = 12 – делится нацело на 3.
№ 11. Запишите все числа, являющиеся делителями каждого из чисел: 1) 15 и 20; 2) 7 и 21; 3) 24 и 36; 4) 20 и 21.
Правильный ответ: 1) делитель 15 и 20 ⇒ 1,5; 2) делитель 7 и 21 ⇒ 1,7; 3) делители 24 и 36 ⇒ 1, 2, 3, 4, 6, 12; 4) делитель 20 и 21 ⇒ 1.
№ 12. Запишите все числа, являющиеся делителями каждого из чисел: 1) 12 и 18; 2) 60 и 90; 3) 22 и 35; 4) 9 и 27.
Правильный ответ: 1) делители 12 и 18 ⇒ 1, 2, 3, 6;
2) делители 60 и 90 ⇒ 1, 2, 3, 5, 6, 10, 15, 30;
3) делитель 22 и 35 ⇒ 1;
4) делители 9 и 27 ⇒ 1, 3, 9.
№ 13. Запишите какое-либо число, кратное каждому из чисел: 1) 3 и 4; 2) 6 и 12; 3) 4 и 6.
Правильный ответ: Число, кратное каждому из чисел: 1) 3 и 4 ⇒ 12; 2) 6 и 12 ⇒ 24; 3) 4 и 6 ⇒ 48.
№ 14. Запишите какое-либо число, кратное каждому из чисел: 1) 5 и 9; 2) 8 и 32; 3) 8 и 12.
Правильный ответ: Число, кратное каждому из чисел: 1) 5 и 9 ⇒ 45; 2) 8 и 32 ⇒64; 3) 8 и 12 ⇒ 24.
№ 15. Запишите: 1) все двузначные числа, кратные 19; 2) все трёхзначные числа, кратные 105.
Правильный ответ: 1) все двузначные числа, кратные 19: 19, 38, 57, 76, 95;
2) все трехзначные числа, кратные 105: 105, 210, 315, 420, 525, 630, 735, 840, 945.
№ 16. Запишите все двузначные числа, кратные 23.
Правильный ответ: Все двузначные числа, кратные 23: 23, 46, 69, 92.
№ 17. Запишите все значения х, кратные числу 4, при которых верно неравенство 18 < х < 36.
Правильный ответ: 18 < х < 36 верно при х = 20, 24, 28, 32.
№ 18. Запишите все значения х, кратные числу 6, при которых верно неравенство 25 < х < 60.
Правильный ответ: 25 < х < 60 верно при х = 30, 36, 42, 48, 54.
№ 19. Запишите все значения х, являющиеся делителями числа 80, при которых верно неравенство 7 < х < 40.
Правильный ответ: 7 < х < 40 верно при х = 8, 10, 16, 20.
№ 20. Запишите все значения х, являющиеся делителями числа 98, при которых верно неравенство 14 < х < 50.
Правильный ответ: 14 < х < 50 верно при х = 49.
№ 21. Найдите число, кратное числам 9 и 11, которое больше 100. Сколько существует таких чисел?
Правильный ответ: Число, кратное 9 и 11, которое больше 100: 198. Таких чисел бесконечное множество.
№ 22. Найдите число, кратное числам 9 и 12, которое меньше 100. Сколько существует таких чисел?
Правильный ответ: Число, кратное числам 9 и 12, которое меньше 100: 36, 72. Всего 2 таких числа.
№ 23. Верно ли утверждение: 1) если число а кратно 6, то оно кратно 3;
2) если число а кратно 3, то оно кратно 6;
3) если число а кратно числам 3 и 4, то оно кратно 12;
4) если число а кратно числам 4 и 6, то оно кратно 24?
Ответ проиллюстрируйте примерами.
Правильный ответ: 1) если число а кратно 6, то оно кратно 3 — верно;
2) если число а кратно 3, то оно кратно 6 — НЕверно;
3) если число а кратно числам 3 и 4, то оно кратно 12 — верно;
4) если число а кратно числам 4 и 6, то оно кратно 24 — НЕверно.
№ 24. Найдите три натуральных числа, для которых кратным будет число: 1) 65; 2) 121. Укажите все варианты выбора таких трёх чисел.
Правильный ответ: 1) кратным 65: 1, 5, 13, 65 (65 = 5 • 13). 4 варианта: 1-5-13, 1-5-65, 1-13-65, 5-13-65.
2) кратным 121: 1, 11, 121 (121 = 11 • 11). 1 вариант.
№ 25. При делении числа а на 7 получили остаток 4. Какому условию должно удовлетворять число b, чтобы сумма а + b была кратна 7?
Правильный ответ: наименьшее: b = 3, а каждое последующее на 7 больше: 10, 17, 24, …
№ 26. При делении числа а на 9 получили остаток 5. Какому условию должно удовлетворять число b, чтобы разность а – b была кратна 9?
Правильный ответ: наименьшее: b = 5, а каждое последующее на 9 больше: 14, 23, 32, …
№ 27. При каких натуральных значениях n значение выражения 15n кратно числу: 1) 3; 2) 5; 3) 10; 4) 11?
Правильный ответ: 1) 15n кратно числу 3: n – любое число, так как 15 кратно 3;
2) 15n кратно числу 5: n – любое число, так как 15 кратно 5;
3) 15n кратно числу 10: n – четное число, чтобы произведение;
4) 15n кратно числу 11: n – кратно 11.
№ 28. При каких натуральных значениях n значение выражения: 1) 3n + 2 кратно числу 2; 2) 4n + 3 кратно числу 3?
Правильный ответ: 1) 3n + 2 кратно 2: n = 0 и четные. 2) 4n + 3 кратно 3: n – кратные 3.
№ 29. Докажите, что: 1) двузначное число, записанное двумя одинаковыми цифрами, кратно 11;
2) трёхзначное число, записанное тремя одинаковыми цифрами, кратно 37.
Правильный ответ: 1) Такое число можно представить в виде произведений двух множителей, один из которых 11 ⇒ Произведение кратно 11. Пример: 55 = 11 • 5.
2) Такое число можно представить в виде произведения двух множителей, один из которых 111, а 111 = 3 • 37 ⇒ произведение кратно 37. Пример: 888 = 111 • 8 = 3 • 37 • 8.
№ 30. К однозначному числу дописали одну цифру, в результате чего оно увеличилось в 41 раз. Какую цифру и к какому числу дописали?
Правильный ответ: цифру 4 дописали слева к числу 1 (получилось 41) или цифру 8 дописали слева к числу 2 (получилось 82).
№ 31. В двузначном числе зачеркнули одну цифру, в результате чего оно уменьшилось в 17 раз. Какую цифру и в каком числе зачеркнули?
Правильный ответ: цифру 7 зачеркнули в числе 17 (получилось 1) или цифру 8 в числе 85 (получилось 5).
№ 32. Первая на Руси школа, как написано в «Повести временных лет», была открыта в Киеве в 988 г. при князе Владимире Святославиче. В 1701 г. указом императора Петра I была создана первая в России государственная светская школа – Школа математических и навигацких наук, или, как чаще её называли, Навигацкая школа. Первоначально школу возглавил боярин Фёдор Головин, а затем – выдающийся русский математик–педагог Леонтий Филиппович Магницкий (1669–1739), проработавший в школе 38 лет – со дня её открытия в 1701 г. до последних дней своей жизни. Перу Л.Ф. Магницкого принадлежал первый изданный в России в 1703 г. учебник по математике, на долгие годы ставший основным учебником российских школ. В Навигацкой школе обучали чтению, письму, арифметике, геометрии, тригонометрии, черчению, географии, астрономии, навигации и другим предметам. Через сколько лет после открытия первой на Руси школы была открыта Навигацкая школа? На сколько лет ваша школа «младше» Навигацкой школы?
№ 33. Упростите выражение и вычислите его значение: 1) 0,2а • 50b, если а = 4, b = 3,6; 2) 0,4x • 25y, если x = 2,4, у = 3.
Правильный ответ: 1) 0,2а • 50b = 10аb при а = 4, b = 3,6: 10 • ab = 10 • 4 • 3,6 = 4 • 36 = 144;
2) 0,4x • 25у = 10xу при х = 2,4; у = 3: 10 • xу = 10 • 2,4 • 3 = 24 • 3 = 72.
№ 34. Решите уравнение: 1) 2,48x + 3,52x = 1,26; 2) 4,63x + 3,37x = 1,92.
№ 35. В столовую завезли 146 кг овощей: 6 ящиков помидоров и 8 ящиков огурцов. Найдите, сколько килограммов огурцов было в каждом ящике, если помидоров в каждом ящике было 7,8 кг, а масса огурцов во всех ящиках одинакова.
№ 36. Запишите в виде суммы разрядных слагаемых число: 1) 278; 2) 5 093.
Правильный ответ: 1) 278 = 200 + 70 + 8; 2) 5093 = 5000 + 90 + 3.
№ 37. Выполните деление с остатком: 1) 429 : 2; 2) 5 001 : 2; 3) 768 : 10; 4) 9 123 : 10; 5) 134 : 5; 6) 2 867 : 5.
№ 38. Выразите делимое через неполное частное, делитель и остаток в виде равенства а = bq + r, где а – делимое, b – делитель, q – неполное частное, r – остаток: 1) 83 : 7; 2) 171 : 17.
Правильный ответ: 1) 83 : 7 = 11 (ост. 6) ⇒ 83 = 7 • 11 + 6.
2) 171 : 17 = 10 (ост. 1) ⇒ 171 = 17 • 10 + 1.
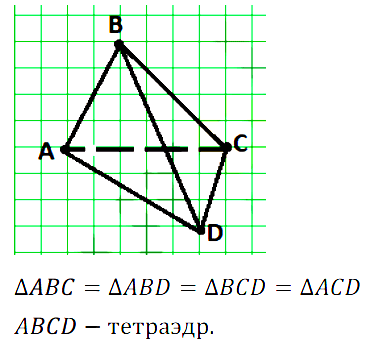
№ 39. Сложите из шести спичек четыре равносторонних треугольника со стороной, равной длине одной спички.
в ОГЛАВЛЕНИЕ (2021 год) Упражнения 40 — 72
Вы смотрели: Упражнения по математике для УМК Мерзляк с ответами на некоторые задачи. §1. Делители и кратные (2019, 2020, 2021 годы). Математика 6 Мерзляк. Упражнения 01-39. ГДЗ Учебник (Решебник упражнений).