Упражнения по математике для УМК Мерзляк с ответами на некоторые задачи. §4. Простые и составные числа (2019, 2020, 2021 годы). Математика 6 Мерзляк. Упражнения 104-137.
ОГЛАВЛЕНИЕ (2021 г.) ТЕОРИЯ: § 4.
Математика 6 Мерзляк (2021 год)
Упражнения 104-137
№ 104. Среди чисел 1, 3, 6, 7, 12, 13, 21, 23, 24, 28, 29, 33, 45, 46, 47 укажите: 1) простые; 2) составные.
Правильный ответ: 1) Простые числа: 3, 7, 13, 23, 29, 47. 2) Составные числа: 6, 12, 21, 24, 28, 33, 45, 46.
№ 105. Запишите все делители данного числа, подчеркните те из них, которые являются простыми числами: 1) 21; 2) 30; 3) 48; 4) 54.
Правильный ответ: 1) делители числа 21: 1, 3, 7, 21.
2) делители числа 30: 1, 2, 3, 5, 6, 10, 15, 30.
3) делители числа 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
4) делители числа 54: 1, 2, 3, 6, 9, 18, 27, 54.
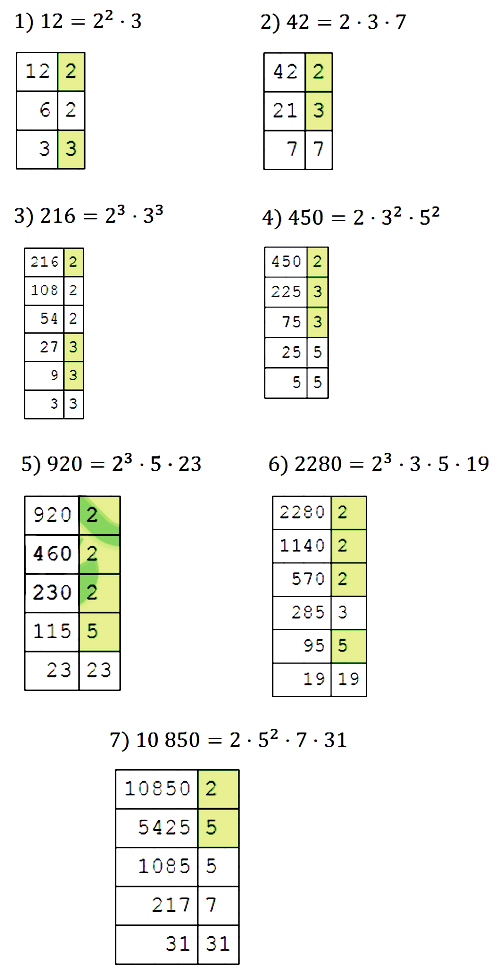
№ 106. Разложите на простые множители число: 1) 12; 2) 42; 3) 216; 4) 450; 5) 920; 6) 2 280; 7) 10 850.
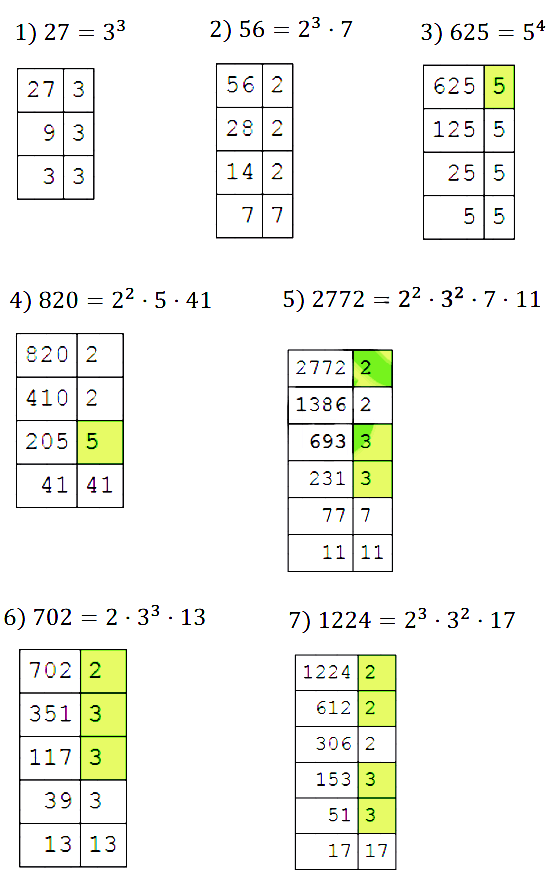
№ 107. Разложите на простые множители число: 1) 27; 2) 56; 3) 625; 4) 820; 5) 2 772; 6) 702; 7) 1 224.
№ 108. Запишите: 1) все простые числа, которые больше 10 и меньше 25; 2) все составные числа, которые больше 35 и меньше 49.
Правильный ответ: 1) Простые числа, больше 10, но меньше 25: 11, 13, 17, 19, 23.
2) Составные числа, больше 35, но меньше 49: 36, 38, 39, 40, 42, 44, 45, 46, 48.
№ 109. Запишите: 1) все простые числа, которые больше 22 и меньше 38; 2) все составные числа, которые больше 60 и меньше 78.
Правильный ответ: 1) Простые числа, которые больше 22 и меньше 38: 23, 29, 31, 37.
2) Составные числа, которые больше 60 и меньше 78: 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77.
№ 110. Простым или составным числом является произведение: 1) 13 • 1; 2) 14 • 1; 3) 4 • 7; 4) 11 • 13; 5) 43 • 1; 6) 1 • 111 ?
Правильный ответ: 1) 13 • 1 => простое.
2) 14 • 1 => составное.
3) 4 • 7 => составное.
4) 11 • 13 => составное.
5) 43 • 1 => простое.
6) 1 • 111 => составное.
№ 111. Запишите все делители числа, равного произведению: 1) 2 • 2 • 5; 2) 3 • 5 • 7.
Правильный ответ: 1) 2 • 2 • 5 = 20 => Делители: 1, 2, 4, 10, 5, 20.
2) 3 • 5 • 7 = 105 => Делители: 1, 3, 5, 7, 15, 21, 35, 105.
№ 112. Запишите все делители числа, равного произведению: 1) 2 • 5 • 13; 2) 3 • 3 • 3 • 7.
Правильный ответ: 1) 2 • 5 • 13 = 130 => Делители: 1, 2, 5, 10, 13, 26, 65, 130.
2) 3 • 3 • 3 • 7 = 189 => Делители: 1, 3, 7, 9, 21, 27, 63, 189.
№ 113. Чему равно частное от деления числа а на число b, если: 1) а = 2 • 2 • 2 • 3 • 3 • 7, b = 2 • 2 • 3 • 7; 2) а = 3 • 5 • 5 • 13 • 17 • 19, b = 3 • 13 • 19 ?
Правильный ответ: 1) Если а = 2 • 2 • 2 • 3 • 3 • 7; b = 2 • 2 • 3 • 7, то a : b = 2 • 2 • 2 • 3 • 3 • 7 : 2 : 2 : 3 : 7 = 6.
2) Если а = 3 • 5 • 5 • 13 • 17 • 19; b = 3 • 13 • 19, то а : b = 3 • 5 • 5 • 13 • 17 • 19 : 3 : 13 : 19 = 425.
№ 114. Чему равно частное от деления числа а на число b, если: 1) а = 2 • 3 • 5 • 5 • 7 • 11 • 13, b = 2 • 5 • 13; 2) а = 2 • 2 • 3 • 5 • 23 • 37, b = 2 • 3 • 37 ?
Правильный ответ: 1) Если а = 2 • 3 • 5 • 5 • 7 • 11 • 13; b = 2 • 5 • 13, то a : b = 2 • 3 • 5 • 5 • 7 • 11 • 13 : 2 : 5 : 13 = 1155.
2) Если а = 2 • 2 • 3 • 5 • 23 • 37; b = 2 • 3 • 37, то a : b = 2 • 2 • 3 • 5 • 23 • 37 : 2 : 3 : 37 = 230.
№ 115. Запишите все двузначные числа, в разложении которых на простые множители один из множителей равен: 1) 7; 2) 17; 3) 23.
Правильный ответ: 1) Один из множителей равен 7: 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98.
2) Один из множителей равен 17: 17, 34, 51, 68, 85.
3) Один из множителей равен 23: 23, 46, 69, 92.
№ 116. Запишите все двузначные числа, разложение которых на простые множители состоит: 1) из двух одинаковых множителей; 2) из трёх одинаковых множителей.
Правильный ответ: 1) состоящие из двух одинаковых множителей: 16 = 4 • 4; 25 = 5 • 5; 36 = 6 • 6; 49 = 7 • 7; 64 = 8 • 8; 81 = 9 • 9.
2) состоящие из трех одинаковых множителей: 27 = 3 • 3 • 3; 64 = 4 • 4 • 4.
№ 117. Сколько существует чисел, которые можно разложить на два двузначных простых множителя, один из которых на 2 больше другого? Воспользуйтесь таблицей простых чисел.
Правильный ответ: 6 чисел (143 = 11 • 13; 323 = 17 • 19; 899 = 29 • 31; 1763 = 41 • 43; 3599 = 59 • 61; 5183 = 71 • 73).
№ 118. Найдите все числа, которые можно разложить на два двузначных простых множителя, разность которых равна 4. Воспользуйтесь таблицей простых чисел.
Правильный ответ: 6 чисел (221 = 13 • 17; 437 = 19 • 23; 1517 = 37 • 41; 2021 = 43 • 47; 4757 = 67 • 71; 6557 = 79 • 83).
№ 119. Задумали простое число. Известно, что следующее за ним натуральное число тоже простое. Какое число задумали?
Правильный ответ: Задумали число 2. Следующее число 3 – простое.
№ 120. Может ли сумма двух простых чисел быть простым числом? В случае утвердительного ответа приведите пример.
Правильный ответ: Да, может. 2 + 3 = 5.
№ 121. Может ли быть простым числом: 1) произведение двух различных чисел; 2) значение площади квадрата, длина стороны которого выражается натуральным числом? Ответ обоснуйте.
Правильный ответ: 1) Да, может. 13 • 1 = 13 => одно число простое, а второе – 1.
2) Нет, так как у площади квадрата есть делители, кроме 1 и самой площади.
№ 122. Может ли сумма двух составных чисел быть простым числом? В случае утвердительного ответа приведите примеры.
Правильный ответ: Да, может. 13 = 4 + 9; 17 = 8 + 9; 19 = 9 + 10.
№ 123. Существует ли прямоугольник, длины сторон которого выражаются натуральными числами, а периметр – простым числом (длины сторон и периметр прямоугольника выражены в одних и тех же единицах измерения)? Ответ обоснуйте.
Правильный ответ: Нет. Р = 2 • (а + b) ⇒ периметр – это четное число ⇒ периметр не может быть простым числом.
№ 124. Может ли произведение ста различных простых чисел делиться нацело: 1) на 3; 2) на 9?
Правильный ответ: 1) На 3: да, если один из множителей равен 3.
2) На 9: нет, так как 9 = 3 • 3 ⇒ значит, в произведении должно быть два одинаковых числа 3, чтобы оно делилось на 9.
№ 125. Существуют ли три последовательных натуральных числа: 1) каждое из которых является простым; 2) ни одно из которых не является составным? Ответ обоснуйте.
Правильный ответ: 1) Нет, так как из трех последовательных чисел хотя бы одно – четное ==> оно не является простым.
2) Да. Например: 1, 2, 3.
№ 126. При каком натуральном значении п будет простым числом значение выражения: 1) 2n; 2) n2; 3) n(n + 1)?
Правильный ответ: 1) 2n; при n = 1. 2) n2; таких n – нет. 3) n(n + 1); при n = 1.
№ 127. Натуральное число а, которое больше 1 и меньше 100, не делится нацело ни на одно из чисел 2, 3, 5 и 7. Верно ли, что число а – простое? Ответ обоснуйте.
Правильный ответ: Да, так как оно не делится на 2 ⇒ число нечетное и, значит, оно не делится на 4, 6, 8 и 9 ⇒ то есть не делится ни па одно из чисел первой десятки. A так как число меньше 100, то его можно представить только в виде 1 • а ⇒ а – простое.
№ 128. Простое число, большее 1 000, поделили на 6. Чему может быть равным остаток?
Правильный ответ: Остаток может быть равен 1 или 5, в противном случае число было простым.
№ 129. Найдите все пары простых чисел, разность которых равна 17.
Правильный ответ: 2 и 19 ⇒ одна пара чисел.
№ 130. Найдите количество делителей числа, равного значению выражения: 1) 24; 2) 23 • З2; 3) 2n • 3m, m и n – натуральные числа.
Правильный ответ: 1) 24 = 16. Делители числа 16: 1, 2, 4, 8, 16 (5 чисел).
2) 23 • 32 = 8 • 9 = 72. Делители числа 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 (12 чисел).
3) 2n • 3m; где m и n – натуральные числа. (n + 1) • (m + 1) – количество делителей.
№ 131. Решите уравнение: 1) 4x + 5x + 4,7 = 16,4; 2) 0,7x – 0,4x + 46 = 211; 3) (35,8 – x) : 2,1 = 1,3; 4) 0,9(283 – x) = 17,01.
Правильный ответ: 1) 4х + 5х + 4,7 = 16,4 ⇒ 9х = 16,4 – 4,7 ⇒ х = 1,3. Ответ: 1,3.
3) (35,8 – х) : 2,1 = 1,3 ⇒ 35,8 – х = 2,73 ⇒ х = 35,8 – 2,73 = 33,07. Ответ: 33,07.
2) 0,7x – 0,4х + 46 = 211 ⇒ 0,3х = 211 – 46 ⇒ х = 550. Ответ: 550.
4) 0,9 • (283 – х) = 17,01 ⇒ 283 – х = 18,9 ⇒ х = 283 – 18,9 = 264,1. Ответ: 264,1.
№ 132. Запишите пять чисел, кратных: 1) числу 8; 2) числу 18; 3) числу n.
Правильный ответ: 1) Числа, кратные числу 8: 8, 16, 24, 32, 40.
2) Числа, кратные числу 18: 18, 36, 54, 72, 90.
3) Числа, кратные числу n: n; 2n; 3n; 4n; 5n.
№ 133. При делении нацело числа а на 15 получили число, кратное 6. Делится ли нацело число а на 10? Ответ обоснуйте.
Правильный ответ: Да, так как 15 = 5 • 3 и 6 = 2 • 3. Следовательно 2 • 5 = 10.
№ 134. При делении нацело числа а на 6 получили число, кратное 12. Делится ли нацело число а на 9? Ответ обоснуйте.
Правильный ответ: Да, так как 6 = 2 • 3 и 12 = 3 • 4; а 3 • 3 = 9.
№ 135. Найдите значение степени: 1) 34; 2) 62; 3) 53; 4) 27; 5) 73; 6) 112.
Правильный ответ: 1) 34 = 81; 2) 62 = 36; 3) 53 = 125; 4) 27 = 125; 5) 73 = 343; 6) 112 = 121
№ 136. Из чисел 348, 975, 1 026, 2 531, 12 120, 43 674, 58 121 выпишите те, которые делятся нацело: 1) на 2; 2) на 3; 3) на 5.
Правильный ответ: 1) Делятся нацело на 2: 348, 1026, 12 120, 43 674.
2) Делятся нацело на 3: 348, 975, 1026, 12 120, 43 674.
3) Делятся нацело на 5: 975, 12 120.
№ 137. Шахматный конь начинает свой маршрут в левом нижнем углу доски, а заканчивает его в правом верхнем углу. Может ли конь при этом побывать на всех полях доски по одному разу?
Правильный ответ: Нет, так как каждый ход цвет клетки меняется. Каждая четная клетка – белая, а так как закончить должен в правом верхнем углу (черном) за 63 хода, то такого быть не может.
ОГЛАВЛЕНИЕ (2021 год) ДАЛЕЕ: Упражнения 138-162
Вы смотрели: Упражнения по математике для УМК Мерзляк с ответами на некоторые задачи. §4. Простые и составные числа (2019, 2020, 2021 годы). Математика 6 Мерзляк. Упражнения 104-137. ГДЗ по новому учебнику (Решебник упражнений).
номер 116 неправильно решён .
Там сказано «В разложении на простые множетили».
А 6,9и4 это не простые множетили