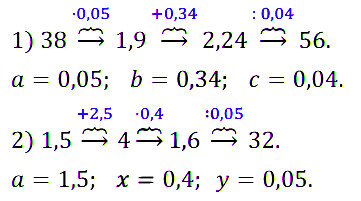Упражнения по математике для УМК Мерзляк с ответами на некоторые задачи. §5. Наибольший общий делитель (2019, 2020, 2021 годы). Математика 6 Мерзляк. Упражнения 138-162.
ОГЛАВЛЕНИЕ (2021 год) ТЕОРИЯ: § 5.
Математика 6 Мерзляк (2021 год)
§ 5. Упражнения 138-162
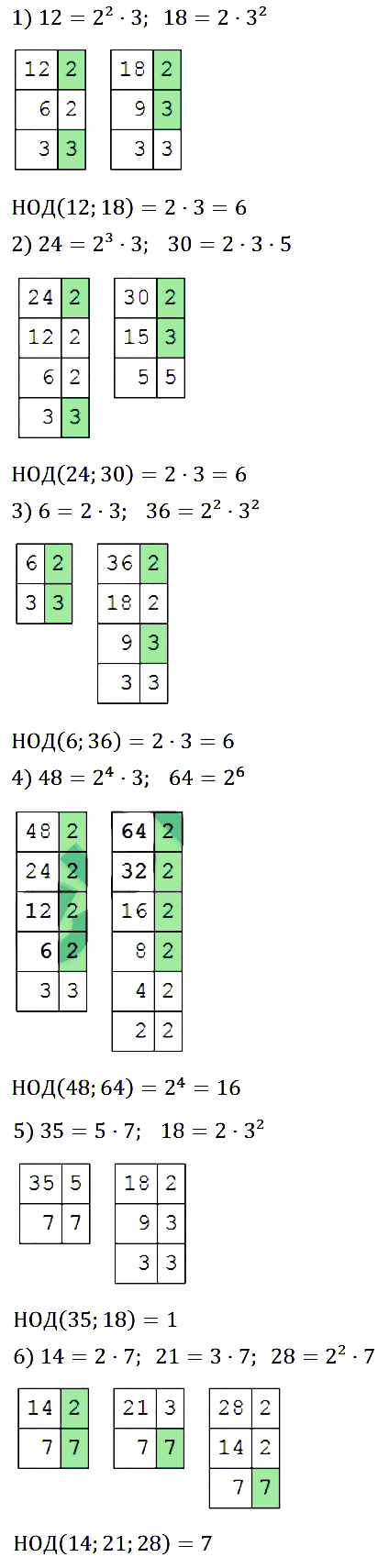
№ 138. Найдите наибольший общий делитель чисел: 1) 12 и 18; 2) 24 и 30; 3) 6 и 36; 4) 48 и 64; 5) 35 и 18; 6) 14, 21 и 28.
Правильный ответ: 1) НОД (12; 18) = 2 • 3 = 6; 2) НОД (24; 30) = 2 • 3 = 6; 3) НОД (6; 36) = 2 • 3 = 6; 4) НОД (48; 64) = 24 = 16; 5) НОД (35; 18) = 1; 6) НОД (14, 21, 28) = 7.
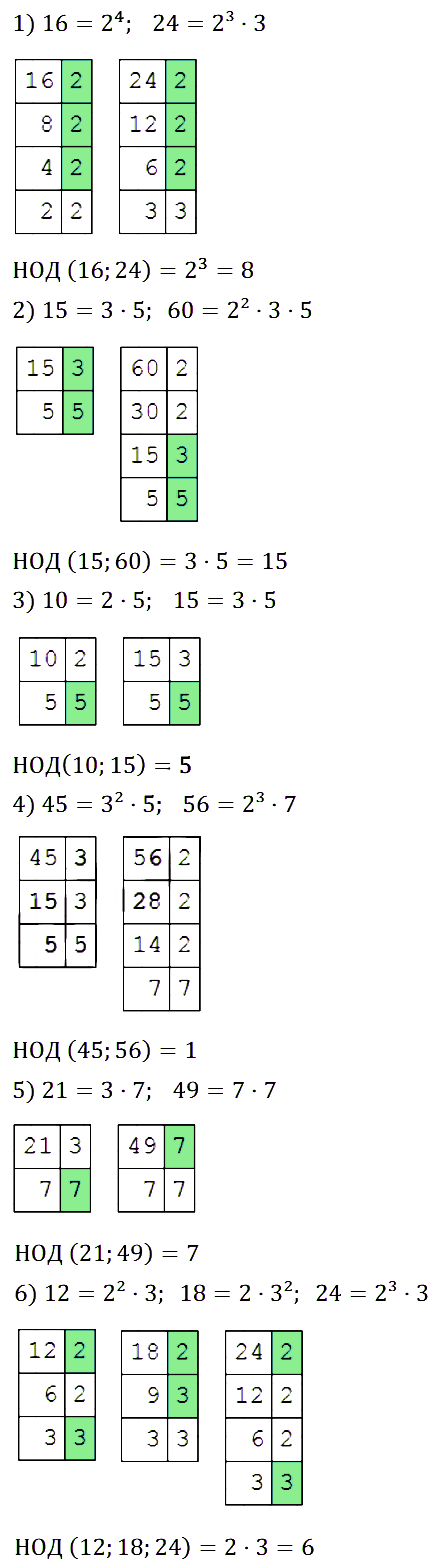
№ 139. Найдите наибольший общий делитель чисел: 1) 16 и 24; 2) 15 и 60; 3)10 и 15; 4) 45 и 56; 5) 21 и 49; 6) 12, 18 и 24.
Правильный ответ: 1) НОД (16; 24) = 23 = 8; 2) НОД (15; 60) = 3 • 5 = 15; 3) НОД (10; 15) = 5; 4) НОД (45; 56) = 1; 5) НОД (21; 49) = 7; 6) НОД (12, 18, 24) = 2 • 3 = 6.
№ 140. Найдите наибольший общий делитель чисел а и b: 1) а = 2 • 2 • 3 • 5 • 7 • 19 и b = 2 • 3 • 3 • 7 • 11 • 13; 2) а = 23 • 32 • 73 • 112 • 19 и b = 22 • 35 • 112 • 193.
Правильный ответ: 1) Если а = 2 • 2 • 3 • 5 • 7 • 19; b = 2 • 3 • 3 • 7 • 11 • 13, то НОД (а; b) = 2 • 3 • 7 = 42.
2) Если а = 23 • 32 • 73 • 112 • 19; b = 22 • 35 • 112 • 193, то НОД (а; b) = 22 • 32 • 112 • 19.
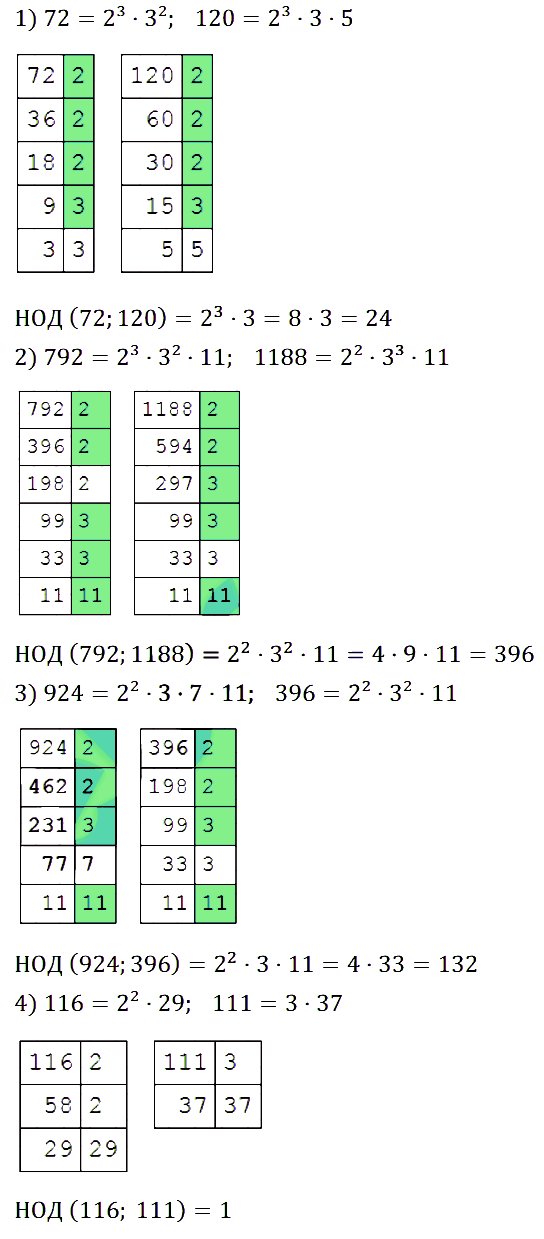
№ 141. Найдите наибольший общий делитель чисел: 1) 72 и 120; 2) 792 и 1188; 3) 924 и 396; 4) 116 и 111.
Правильный ответ: 1) НОД (72; 120) = 23 • 3 = 8 • 3 = 24; 2) НОД (792; 1188) = 22 • 32 • 11 = 4 • 9 • 11 = 396; 3) НОД (924; 396) = 22 • 3 • 11 = 4 • 33 = 132; 4) НОД (116; 111) = 1.
№ 142. Найдите наибольший общий делитель чисел: 1) 42 и 105; 2) 588 и 252; 3) 680 и 612.
Правильный ответ: 1) НОД (42; 105) = 3 • 7 = 21; 2) НОД (588; 252) = 22 • 3 • 7 = 4 • 21 = 84; 3) НОД (680; 612) = 22 • 17 = 68.
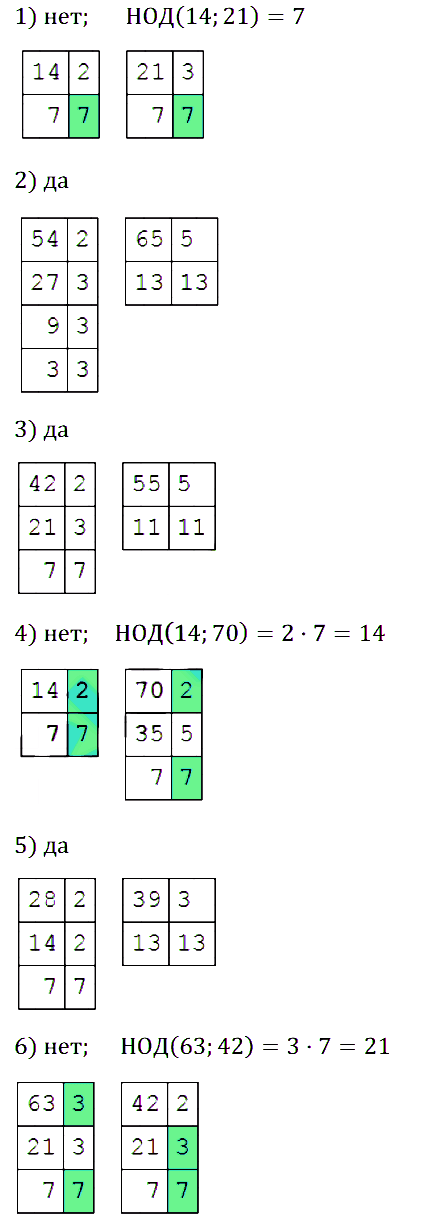
№ 143. Среди данных нар чисел выберите пары взаимно простых чисел: 1) 14 и 21; 2) 54 и 65; 3) 42 и 55; 4) 14 и 70; 5) 28 и 39; 6) 63 и 42. Для пар чисел, не являющихся взаимно простыми, укажите наибольший общий делитель.
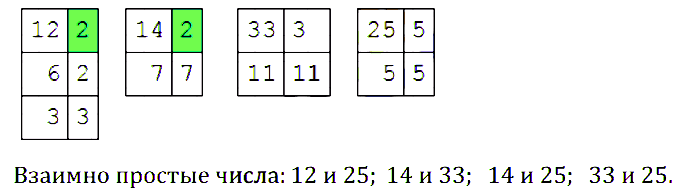
№ 144. Составьте все пары взаимно простых чисел из чисел 12, 14, 33, 25.
Правильный ответ: Взаимно простые числа: 12 и 25; 14 и 33; 14 и 25; 33 и 25.
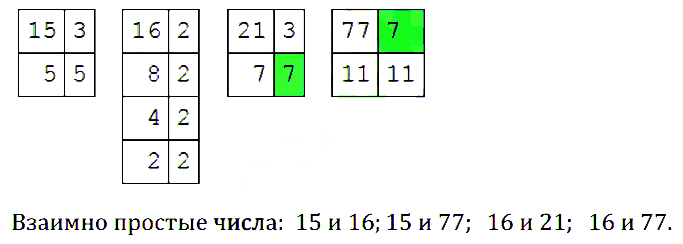
№ 145. Составьте все пары взаимно простых чисел из чисел 15, 16, 21, 77.
Правильный ответ: Взаимно простые числа: 15 и 16; 15 и 77; 16 и 21; 16 и 77.
№ 146. Запишите все правильные дроби со знаменателем 15, у которых числитель и знаменатель – взаимно простые числа.
Правильный ответ: 1/15; 2/15; 4/15; 7/15; 8/15; 11/15; 13/15; 14/15.
№ 147. Запишите все неправильные дроби с числителем 16, у которых числитель и знаменатель – взаимно простые числа.
Правильный ответ: 16/1; 16/3; 16/5; 16/7; 16/9; 16/11; 16/13; 16/15.
№ 148. Докажите, что: 1) числа 364 и 495 – взаимно простые; 2) числа 380 и 399 не являются взаимно простыми.
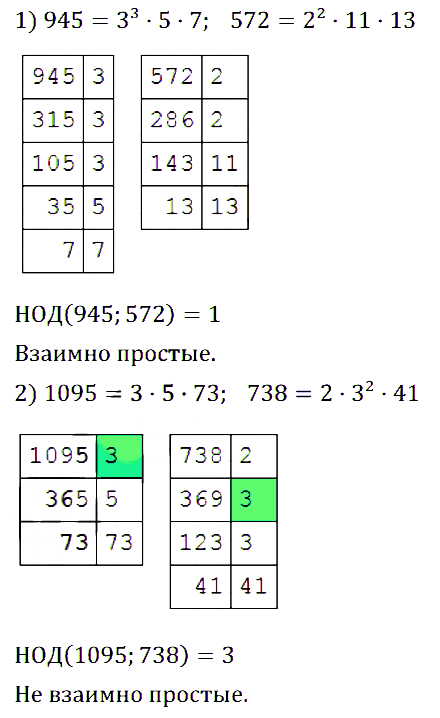
№ 149. Докажите, что: 1) числа 945 и 572 – взаимно простые; 2) числа 1095 и 738 не являются взаимно простыми.
№ 150. Используя цифры 2, 3, 4, запишите все возможные двузначные числа (цифры в каждом двузначном числе должны быть различными). Из полученных чисел выпишите пары взаимно простых чисел.
Правильный ответ: Все двузначные числа: 23, 24, 32, 34, 42, 43.
Взаимно простые: 23 и 24; 23 и 32; 23 и 34; 23 и 42; 23 и 43; 24 и 43; 32 и 43; 34 и 43; 42 и 43.
№ 151. Напишите три пары составных чисел такие, что в парах числа являются взаимно простыми.
Правильный ответ: 8 и 15; 9 и 20; 15 и 22.
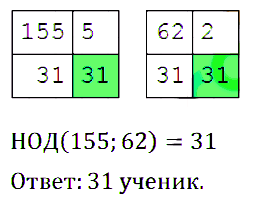
№ 152. Между учениками 6 класса поделили поровну 155 тетрадей и 62 ручки. Сколько в этом классе учеников?
Правильный ответ: 31 ученик.
№ 153. На автомобили погрузили 96 контейнеров с картофелем и 64 контейнера с капустой. Сколько было автомобилей, если известно, что их не меньше 20 и на всех автомобилях было одинаковое количество контейнеров с картофелем и одинаковое количество контейнеров с капустой?
Правильный ответ: 32 автомобиля.
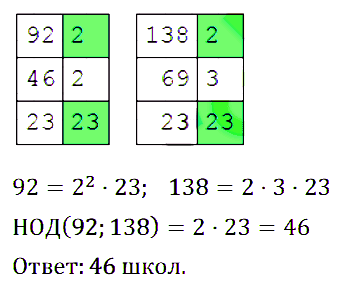
№ 154. Между школьными библиотеками разделили 92 толковых и 138 орфографических словарей русского языка. Сколько было школ, если известно, что их не менее 25 и все школы получили одинаковые комплекты, состоящие из словарей двух видов?
Правильный ответ: 46 школ.
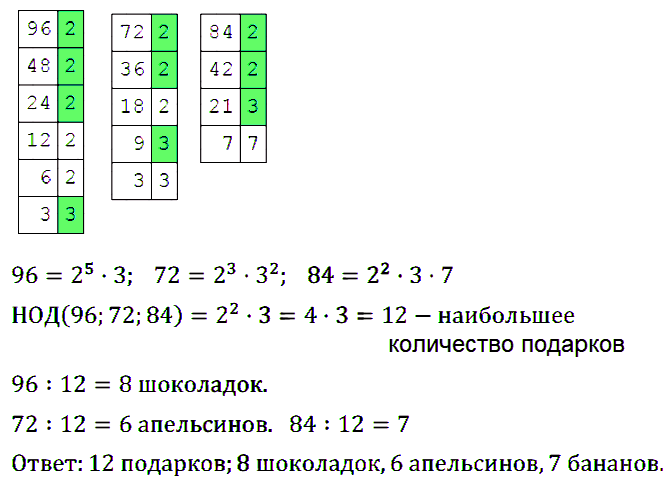
№ 155. Для новогодних подарков приобрели 96 шоколадок, 72 апельсина и 84 банана. Какое наибольшее количество одинаковых подарков можно из них составить, если необходимо использовать все продукты? Сколько в отдельности шоколадок, апельсинов и бананов будет в каждом подарке?
Правильный ответ: 12 подарков; 8 шоколадок, 6 апельсинов, 7 бананов.
№ 156. Из 156 жёлтых, 234 белых и 390 красных роз составляли букеты. Какое наибольшее количество одинаковых букетов можно составить, если необходимо использовать все цветы?
Правильный ответ: 78 букетов.
№ 157. Используя цифры 2, 5 и 9 (цифры не могут повторяться), запишите трёхзначное число, которое: 1) кратно 2; 2) кратно 5. Можно ли с помощью этих цифр записать число, кратное 3?
Правильный ответ: 1) Кратно 2: 592, 952. 2) Кратно 5: 295,925.
Число, кратное 3, записать нельзя, так как 2 + 5 + 9 = 16; а 16 не делится на 3.
№ 158. Какую цифру можно поставить вместо звёздочки в записи 1*8, чтобы полученное число делилось нацело на 18?
Правильный ответ: 108; 198.
№ 159. Запишите число 19 в виде суммы трёх простых чисел.
Правильный ответ: 19 = 3 + 5 + 11.
№ 160. Если к некоторому двузначному числу справа дописать нуль, то данное число увеличится на 432. Найдите это число.
Правильный ответ: 48.
Решение. Пусть число х – было; тогда число 10х – стало. По условию задачи известно, что полученное число на 432 больше данного. Составим уравнение: 10х – х = 432 ⇒ 9х = 432 ⇒ х = 48 – данное число.
№ 161. Найдите числа, которых недостаёт в цепочке вычислений:
1) 38 → •а → 1,9 → +b → 2,24 → :c → 56;
2) а → +2,5 → 4 → •х → 1,6 → :y → 32.
№ 162. Барон Мюнхгаузен рассказывал, что он разрезал арбуз на четыре части, а после того, как его съели, осталось пять корок. Может ли такое быть, если корки не ломать?
Правильный ответ: Такое может быть.
Нужно вырезать сквозной кусок в центре, в форме цилиндра, у которого будет 2 корки – сверху и снизу. Затем оставшуюся часть арбуза разрезать на 3 части – 3 корки. Итого получаем 4 части и 5 корок.
ОГЛАВЛЕНИЕ (2021 год) ДАЛЕЕ: Упражнения 163-186
Вы смотрели: Упражнения по математике для УМК Мерзляк с ответами на некоторые задачи. §5. Наибольший общий делитель (2019, 2020, 2021 годы). Математика 6 Мерзляк. Упражнения 138-162. ГДЗ по новому учебнику (Решебник упражнений).