Упражнения №№ 216-246 по математике в 6 классе из учебника УМК Виленкин с ответами. § 2. Сложение и вычитание дробей с разными знаменателями. 8. Основное свойство дроби. Математика 6 Виленкин. Задачи 216-246. Цитаты из учебника использованы в учебных целях. Ответы адресованы родителям.
Математика 6 класс Виленкин
8. Упражнения 216-246.
№ 216. Используя рисунок 9, объясните, почему равны дроби: 3/5 = 9/15; 3/4 = 12/16; 5/7 = 10/14.
№ 217. По рисунку 10 объясните, почему равны дроби: a) 1/4 = 3/12 = 15/60; …
№ 218. Поясните с помощью часов, почему: а) 2/3 = 8/12 = 40/60; …
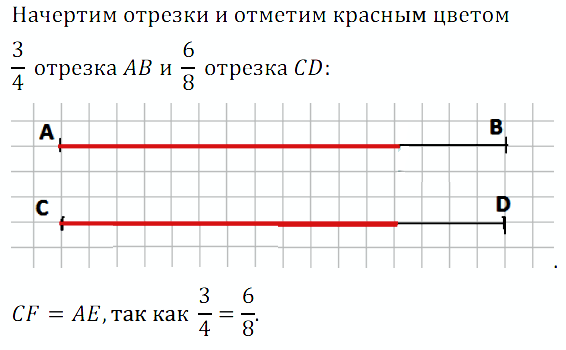
№ 219. Начертите два отрезка АВ и CD длиной по 8 см. Отметьте цветным карандашом 3/4 отрезка АВ и 6/8 отрезка CD. Сравните с помощью циркуля цветные части отрезков АВ и CD.
№ 220. Начертите координатный луч, приняв за единичный отрезок 18 клеток тетради. Отметьте на координатном луче точки с координатами 1/9, 2/9, 3/9, 4/9, 5/9, 6/9, 7/9, 8/9, 1/6, 2/6, 3/6, 4/6, 5/6, 1/3, 2/3. Какие из этих чисел изображаются на координатном луче одной и той же точкой? Запишите соответствующие равенства.
№ 221. Умножьте числитель и знаменатель каждой дроби 1/5, 3/7, 25/8, 39/40 на 5. Напишите соответствующие равенства.
№ 222. Разделите числитель и знаменатель каждой дроби 6/3, 9/6, 15/9, 21/33 на 3. Запишите соответствующие равенства.
№ 223. Сколько двенадцатых долей содержится в 1/4, 1/6, 3/4, 5/6, 2/3?
№ 224. Объясните, почему верно равенство: а) 4/5 = 8/10, б) 44/100 = 11/25.
№ 225. Запишите в виде обыкновенных дробей частные: 3 : 8; 12 : 32; 20 : 48; 5:12. Какие из полученных дробей равны?
№ 226. Какое натуральное число надо записать вместо буквы, чтобы было верным равенство: а) 14/21 = x/3; б) m/18 = 5/9; в) 17/51 = 1/n; г) 15/y = 5/6 ?
№ 227. Вычислите устно: а) 50 • 10 : 125 • 75 – 160 = ?; …
№ 228. Какое число надо умножить на 3, чтобы получить: 3,3; 33,3; 6,6; 6,66; 0,99; 0,999?
№ 229. Найдите значение выражения:
а) 23 + 2,6; в) (1,6 – 0,7)2;
б) 0,32 + 1,1; г) (0,6 • 0,5 + 0,7)3.
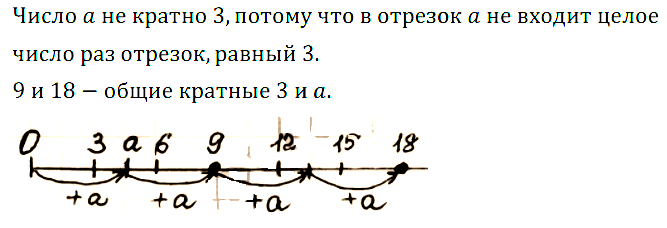
№ 230. На координатном луче (рис. 11) отмечены числа а и 3. Кратно ли число а трём? Отметьте на луче два общих кратных чисел а и 3.
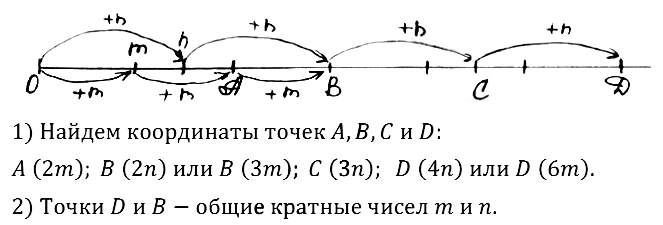
№ 231. Найдите, пользуясь рисунком 12, координаты точек А, В, С и D. Есть ли среди этих точек такие, координаты которых — общие кратные чисел m и n?
№ 232. На сколько процентов увеличится площадь прямоугольника, если его длину увеличить на 30%, а ширину — на 20 %?
№ 233. Составьте программу вычисления на микрокалькуляторе значения выражения: а) 2,85 • (3,27 – 1,45); б) 3,6/(5,41 + 6,59).
№ 234. Найдите методом «решета Эратосфена» все простые числа среди первых ста натуральных чисел.
№ 235. Разложите на простые множители числа: 1) 375; 8505; 41 472; 2) 425; 4225; 8775.
№ 236. Найдите наибольший общий делитель и наименьшее общее кратное чисел: 1) 2450 и 3500; 2) 792 и 2178.
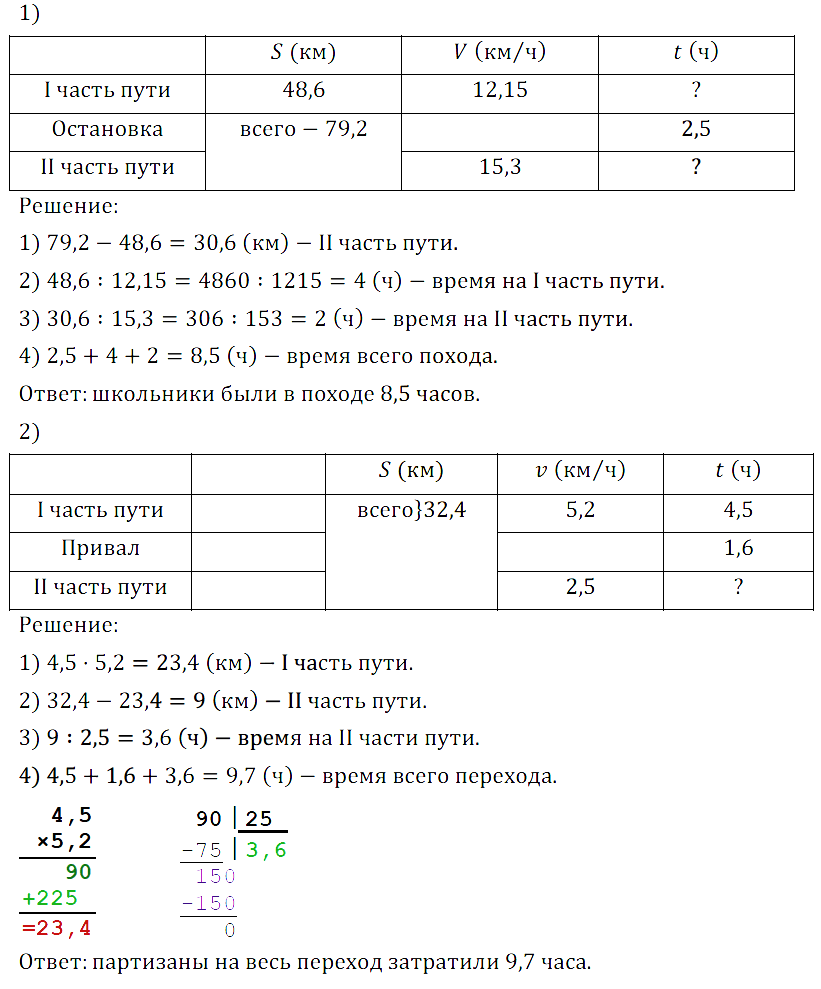
№ 237. Решите задачу:
1) Школьники во время каникул совершили велосипедный поход. Весь путь составил 79,2 км. Первые 48,6 км они двигались со скоростью 12,15 км/ч и сделали привал на 2,5 ч, а потом ехали со скоростью 15,3 км/ч. Сколько времени школьники были в походе?
2) Отряд партизан, выполняя боевое задание, прошёл 32,4 км. Первые 4,5 ч они шли по дороге со скоростью 5,2 км/ч и сделали привал на 1,6 ч, а остальное время они шли по болотистой местности со скоростью 2,5 км/ч. Сколько времени партизаны затратили на весь переход?
№ 238. Составьте задачу по выражению: 1/12; + 5/12.
№ 239. Выполните действия: 8,12 • 0,25 + 3,24 • 0,25.
№ 240. Выполните действия с помощью микрокалькулятора и округлите ответ до сотых: а) 2,835 : 0,225 • 4,537 – 32,929; б) (4,976 + 15,2473) • 2,14 – 5,0784.
№ 241. Из двенадцати лучших бегунов шестого класса нужно отобрать четверых для участия в эстафете. Сколькими способами можно составить такую команду? Сколькими способами четыре члена команды могут распределить между собой этапы эстафеты?
№ 242. Разделите числитель и знаменатель каждой из дробей 18/27, 27/36, 72/63, 45/72 на 9. Напишите соответствующие равенства.
№ 243. Начертите координатный луч, приняв за единичный отрезок длину 12 клеток тетради. Отметьте на луче точки с координатами: 3/4, 1/6, 5/12, 2/3, 9/12, 4/6. Какие из этих чисел являются координатами одной и той же точки?
№ 244. Сколько:
а) шестых долей содержится в 1/2, 1/3, 2/3, 3/2.
б) пятнадцатых долей содержится в 1/5, 2/3, 3/5, 4/3.
№ 245. Найдите наибольший общий делитель и наименьшее общее кратное чисел:
а) 18 и 36; в) 378 и 441;
б) 33 и 44; г) 11 340 и 37 800.
№ 246. Решите уравнение: а) 2,45 • (m – 8,8) = 4,41; б) 7,54k – 3,6k = 5,91.
Вы смотрели: Упражнения по математике для УМК Виленкин с ответами на некоторые задачи. § 2. Сложение и вычитание дробей с разными знаменателями. 8. Основное свойство дроби. Математика 6 Виленкин. Задачи 216-246. ГДЗ по новому учебнику (Решебник упражнений).

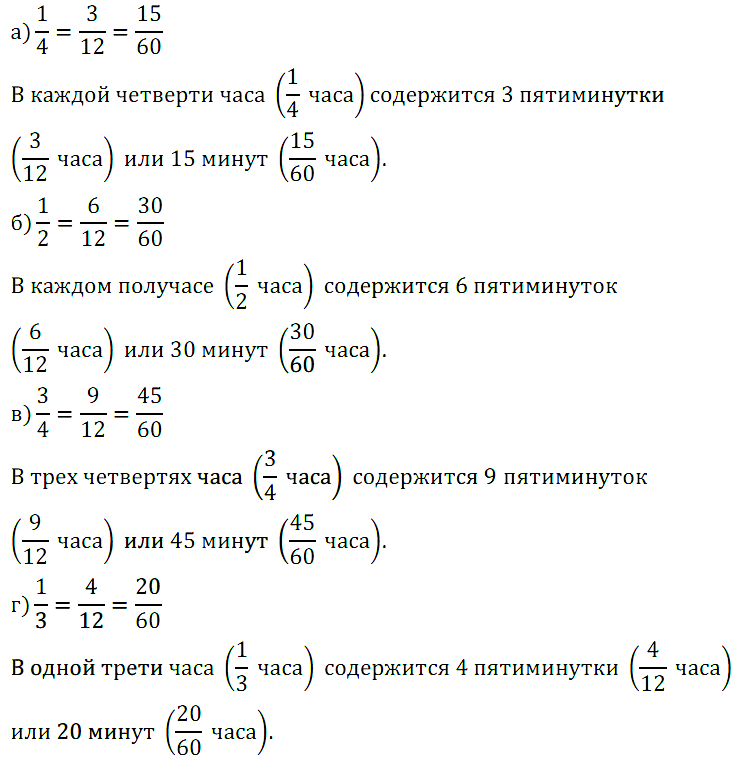
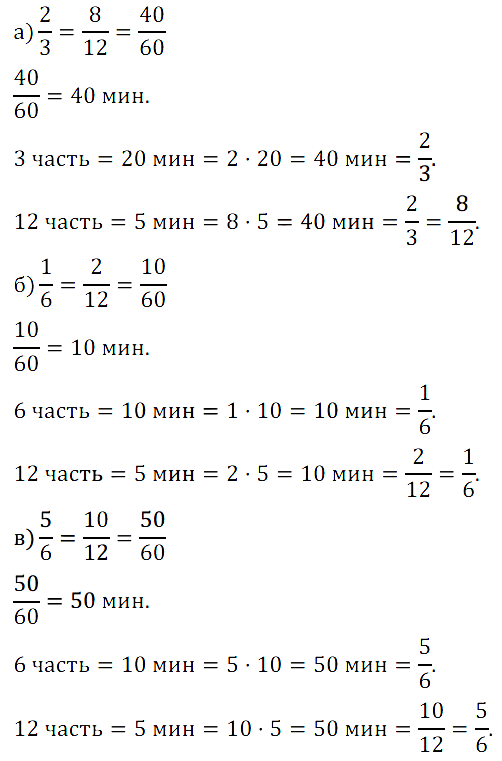
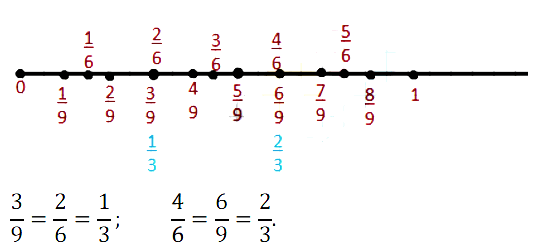
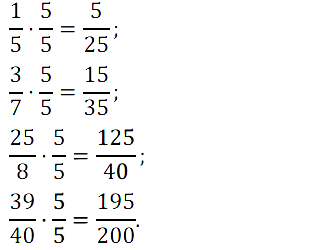
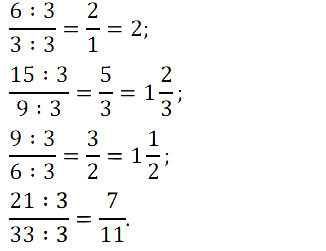
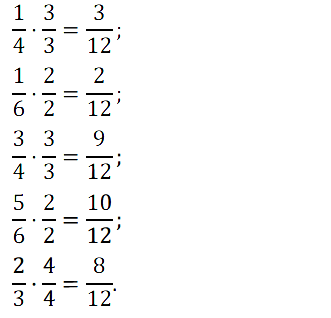

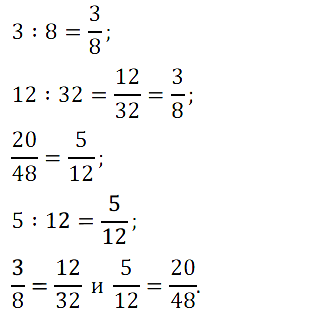
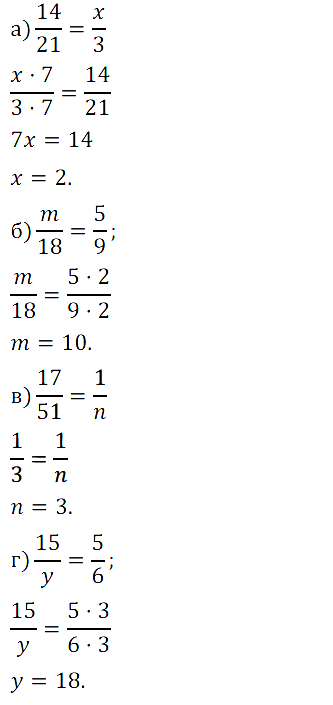
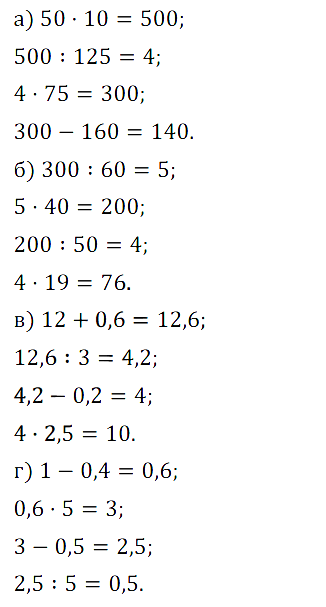
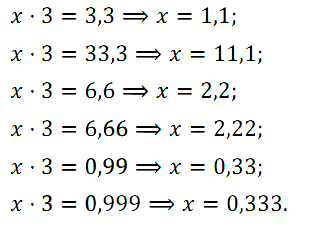
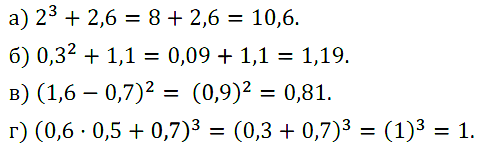

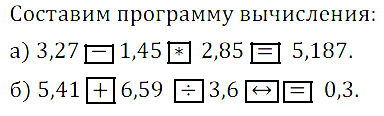

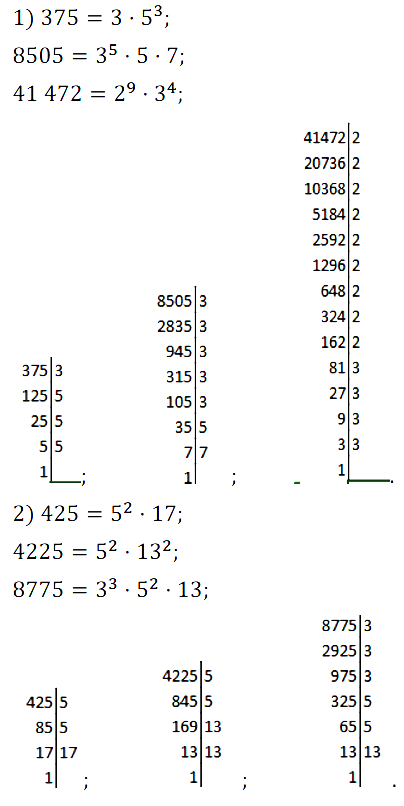


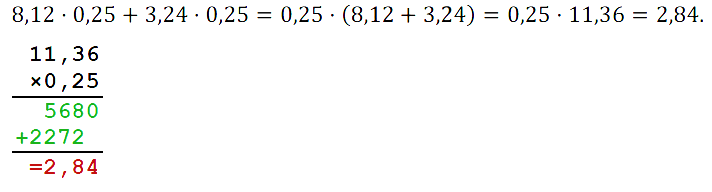
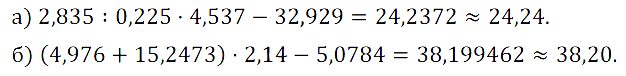

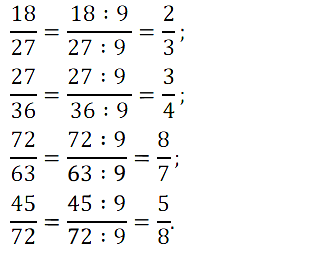
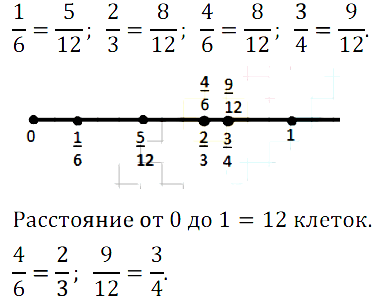
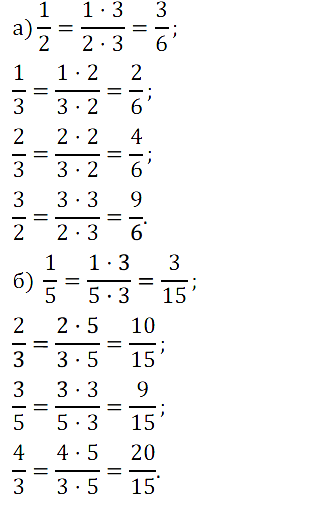

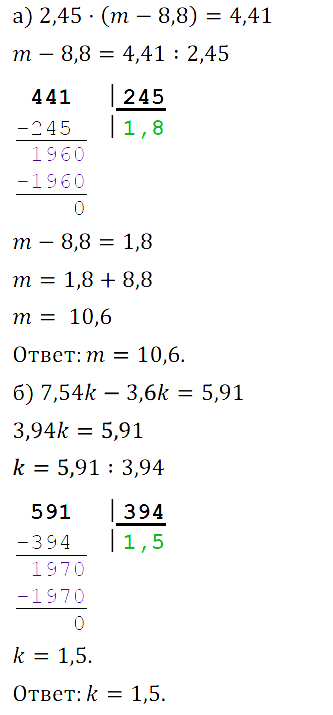
Совсем недавно стала пользоваться вашим учебником с ответами. Спасибо большущее составителю. Очень удобно подобрано по темам.