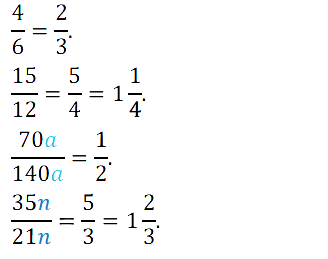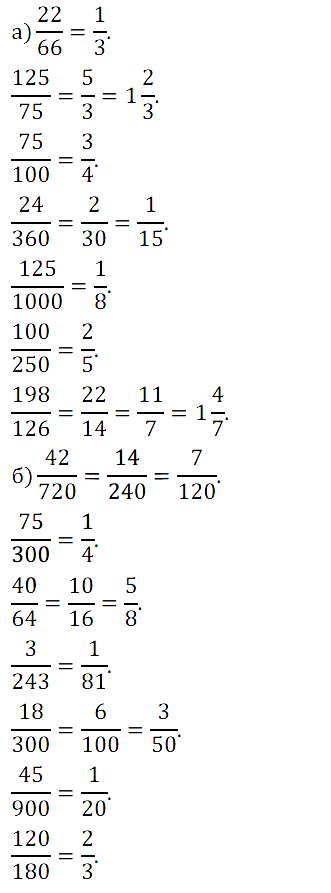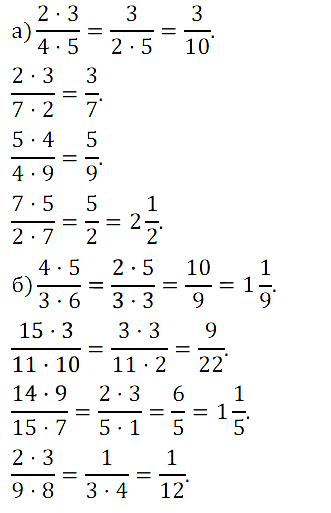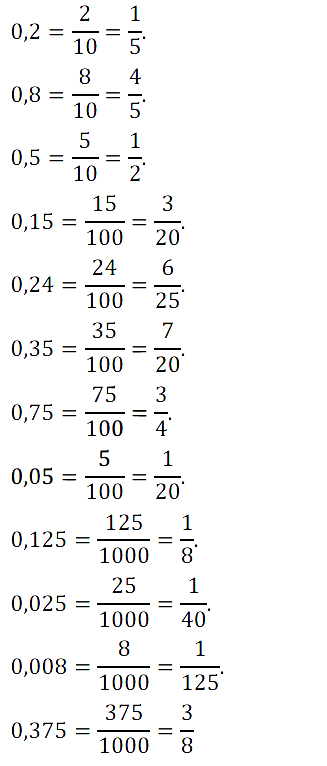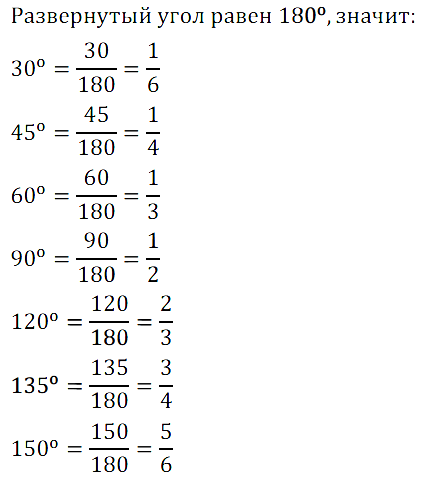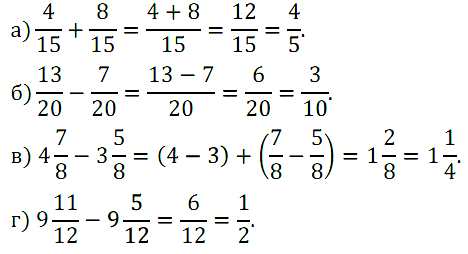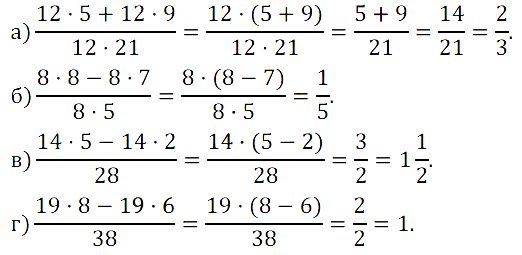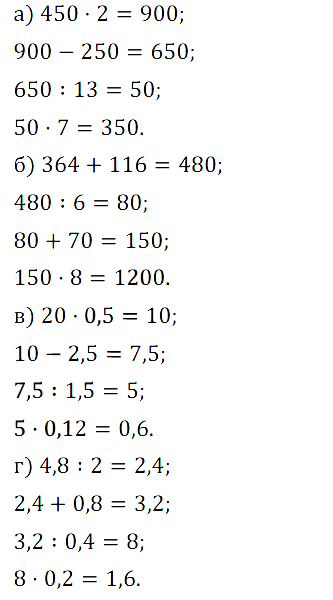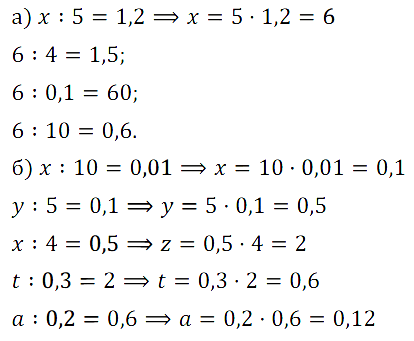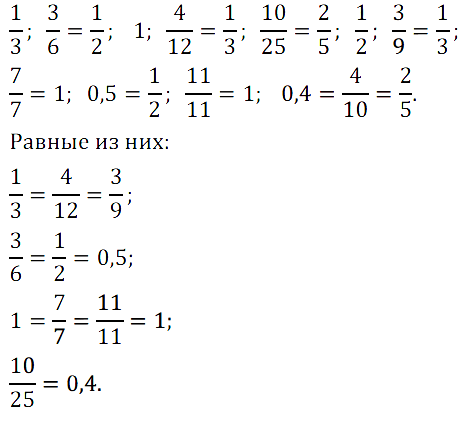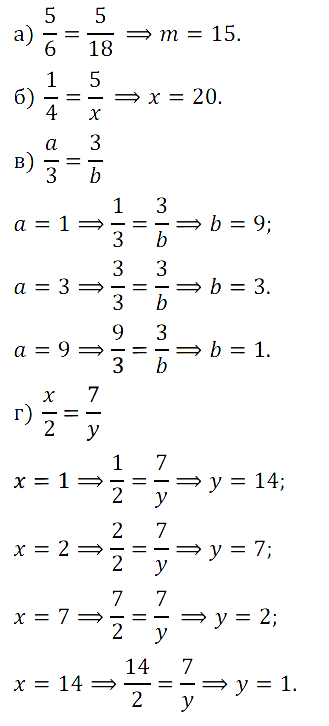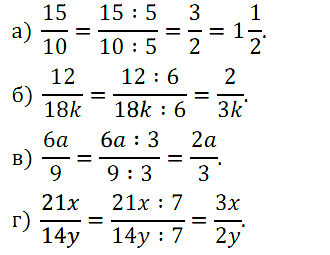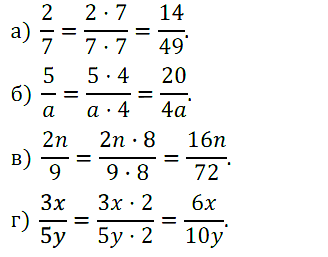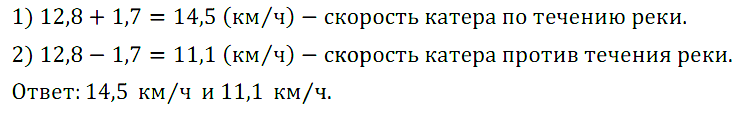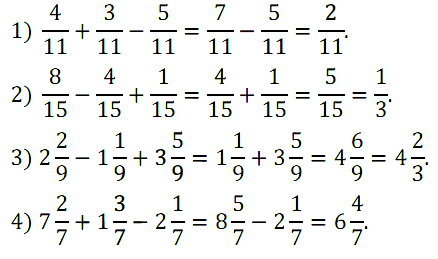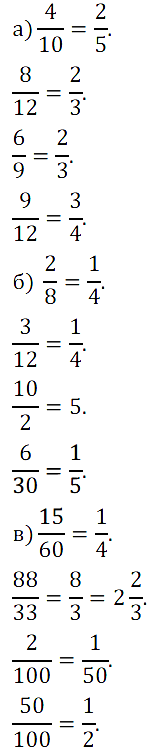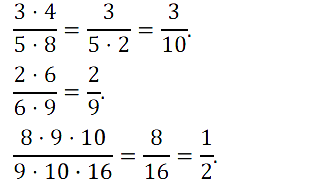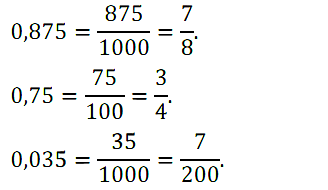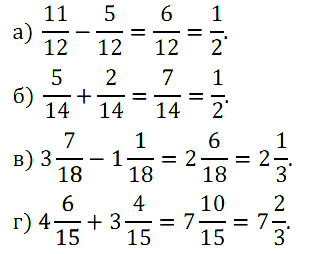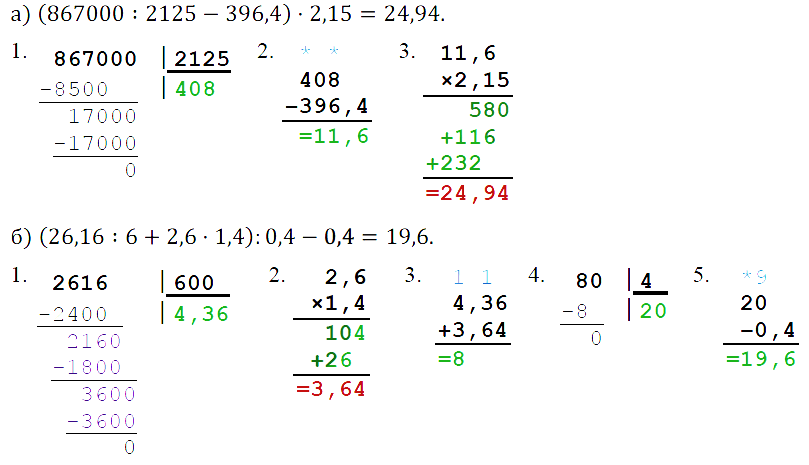Упражнения №№ 247-279 по математике в 6 классе из учебника УМК Виленкин с ответами. § 2. Сложение и вычитание дробей с разными знаменателями. 9. Сокращение дробей. Математика 6 Виленкин. Задачи 247-279. Цитаты из учебника использованы в учебных целях. Ответы адресованы родителям.
Математика 6 класс Виленкин
9. Упражнения 247-279.
№ 247. Сократите дроби: 4/6, 15/12, 70а/140а, 35n/21n.
№ 248. Сократите дроби: a) 22/66, 125/75, 24/360, 125/1000, 100/250, 198/126. б) 42/720, 75/300, 40/64, 3/243, 18/300, 45/900, 120/180.
№ 249. Сократите: a) (2 • 3)/(4 • 5), (2 • 3)/(7 • 2), (5 • 4)/(4 • 9), (7 • 5)/(2 • 7); …
№ 250. Представьте в виде обыкновенной несократимой дроби: 0,2; 0,8; 0,5; 0,15; 0,24; 0,35; 0,75; 0,05; 0,125; 0,025; 0,008; 0,375.
№ 251. Какую часть часа составляют 45 мин, 12 мин, 15 мин, 40 мин, 35 мин?
№ 252. Какую часть развёрнутого угла составляют 30°, 45°, 60°, 90°, 120°, 135°, 150°?
№ 253. Какую часть килограмма составляют 125 г, 250 г, 750 г?
№ 254. Выполните действие: а) 4/15 + 8/15, б) 13/20 – 7/20, в) 4 7/8 – 3 5/8, г) 9 11/12 – 9 5/12.
№ 255. Один рабочий изготовил 16 одинаковых деталей за 6 ч, а другой — 24 такие же детали за 15 ч. Какой из них тратил на изготовление одной детали больше времени и на сколько?
№ 256. Из 20 м ткани сшили 8 одинаковых платьев для взрослых, а из 12 м сшили 8 детских платьев. Сколько метров ткани пошло на одно детское платье и сколько — на одно платье для взрослых?
№ 257. Применив распределительный закон, представьте числитель дроби в виде произведения, а затем сократите: а) (12 • 5 + 12 • 9)/(12 • 21); б) (8 • 8 – 8 • 7)/(8 • 5); …
№ 258. Вычислите устно: а) 450 • 2 – 250 : 13 • 7 = ? …
№ 259. Найдите пропущенные числа: …
№ 260. Найдите среди чисел 1, 3, 10, 12, 13, 15, 16, 39 пары взаимно простых чисел.
№ 261. Найдите равные среди чисел: 1/3; 3/6; 1; 4/12; 10/25; 1/2; 3/9; 7/7; 0,5; 11/11; 0,4.
№ 262. При каких натуральных значениях букв равны дроби a) 5/6 и m/18; б) 1/4 и 5/x; в) a/3 и 3/b; г) x/2 и 7/y.
№ 263. В бригаде 5 рабочих. Зарплата первого рабочего увеличилась на 10%, второго — на 20%, третьего — на 30%, а у четвёртого и пятого осталась прежней. На сколько процентов в среднем выросла зарплата рабочего этой бригады, если раньше все имели одинаковую зарплату?
№ 264. Древнегреческих, а также древнеиндийских математиков интересовали числа, которые соответствовали количеству точек, расположенных в виде некоторой геометрической фигуры — треугольника, квадрата и др. Такие числа называли фигурными. Например, число 10 называли треугольным, число 16 — квадратным (рис. 13). Такое представление помогало древним учёным изучать свойства чисел. Используя рисунок 13, попробуйте найти ещё несколько треугольных и квадратных чисел. Какими свойствами обладают эти числа? Подумайте, как можно находить треугольные и квадратные числа, используя ряд натуральных чисел.
№ 265. Разделите числитель и знаменатель дроби: а) 15/10 на5; б) 12/18k на 6; в) 6а/9 на 3; г) 21х/14у на 7.
№ 266. Умножьте числитель и знаменатель дроби: а) 2/7 на 7; б) 5/а на 4; в) 2n/9 на 8; г) 3x/5y на 2.
№ 267. Сколько пятизначных чисел можно составить из чётных цифр, если цифры в записи числа не повторяются?
№ 268. Собственная скорость катера 12,8 км/ч. Скорость течения реки 1,7 км/ч. Найдите скорость катера по течению и против течения.
№ 269. Скорость движения теплохода по течению реки 22,7 км/ч. Скорость течения 1,9 км/ч. Найдите собственную скорость теплохода и его скорость против течения.
№ 270. Бригада изготовила за 3 дня 6000 деталей при плане 5100 деталей. Причём в первый день была изготовлена треть всех выпущенных деталей, а во второй день — 2/5 плана. Сколько деталей изготовила бригада в третий день?
№ 271. Найдите значение выражения: 1) 4/11 + 3/11 – 5/11; 2) 8/15 – 4/15 + 1/15; …
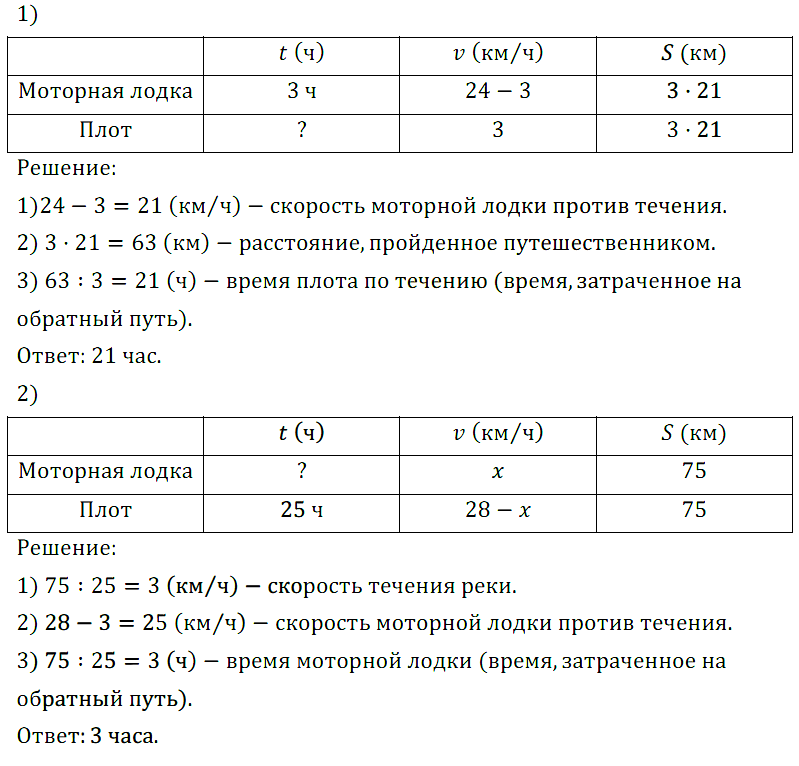
№ 272. Решите задачу: 1) Путешественник проплыл против течения реки на моторной лодке 3 ч. Обратно он вернулся на плоту. Сколько времени путешественник затратил на обратный путь, если собственная скорость лодки 24 км/ч, а скорость течения 3 км/ч? 2) Путешественник проплыл по реке на плоту 75 км за 25 ч. Обратно он вернулся на моторной лодке, собственная скорость которой 28 км/ч. Сколько времени затратил путешественник на обратный путь?
№ 273. Сократите дроби: а) 4/10, 8/12, 6/9, 9/12; б) 2/8, 3/12, 10/2, 6/30; в) 15/60, 88/33, 2/100, 50/100.
№ 274. Сократите: (3 • 4)/(5 • 8), (2 • 6)/(6 • 9), (8 • 9 • 10)/(9 • 10 • 16).
№ 275. Представьте в виде обыкновенной несократимой дроби следующие десятичные дроби: 0,875; 0,75; 0,035.
№ 276. Выполните действие и сократите результат: а) 11/12 – 5/12; б) 5/14 + 2/14; в) 3 7/18 – 1 1/18; г) 4 6/15 + 3 4/15.
№ 277. Турист плыл на теплоходе сначала 1,2 ч по озеру, а затем 3,6 ч по реке, которая впадает в это озеро. Собственная скорость теплохода 22,4 км/ч, а скорость течения реки 1,7 км/ч. Найдите длину всего пути туриста на теплоходе.
№ 278. В четырёх больших и трёх маленьких коробках с цветными карандашами всего 132 карандаша. В двух больших и трёх маленьких таких же коробках всего 84 карандаша. Сколько карандашей в одной маленькой коробке?
№ 279. Выполните действия: а) (867 000 : 2125 – 396,4) • 2,15; б) (26,16 : 6 + 2,6 • 1,4) : 0,4 – 0,4.
Вы смотрели: Упражнения по математике для УМК Виленкин с ответами на некоторые задачи. § 2. Сложение и вычитание дробей с разными знаменателями. 9. Сокращение дробей. Математика 6 Виленкин. Задачи 247-279. ГДЗ по новому учебнику (Решебник упражнений).