Рабочая тетрадь № 1 по математике для 6 класса УМК Мерзляк, Полонский, Якир. Электронная версия. Мерзляк 6 Рабочая тетрадь 1. Цитаты использованы в учебных целях.
Глава 1. Делимость натуральных чисел
§ 1. Делители и кратные
- Заполните пропуски.
1) Натуральное число а делится нацело на натуральное число b, если ______________ ________________ такое, что справедливо равенство __________
2) Если натуральное число а делится нацело на натуральное число b, то число а называют _____________________ числа b, а число b называют ____________________ числа а.
3) Для любого натурального числа а каждое из чисел ______________________, … , является кратным числа а.
4) Наименьшим делителем любого натурального числа а является число _____, а наибольшим —__________________ _______________________
5) Число _____ является делителем любого натурального числа.
6) Наименьшим кратным натурального числа а является________________________
7) Если каждое из чисел а и b делится нацело на число к, то и сумма а + b
8) Если ни число а и ни число b не делятся нацело на число k, то их сумма а + b может _____________________, а может и _____________________ нацело на число k.
9) Если число а делится нацело на число k, а число b ____________________ ___________________, то сумма а + b не делится нацело на число k.
- Подчеркните числа, которые являются делителями числа 36: 3, 4, 6, 8, 9, 10, 12, 15, 18, 24, 36.
- Выберите из чисел 14, 18, 24, 30, 42, 54, 72, 112, 156 те, которые: 1) кратны 6; 2) не кратны 4.
Ответ: 1)____________________; 2)________________________
- Запишите все делители данного числа.
1) Делители 14: __________________ 3) Делители 19:_______
2) Делители 16: __________________ 4) Делители 48:_______
- Запишите какие-либо четыре числа, кратные данному числу.
1) Кратные 4:_____________________ 3) Кратные 19:
2) Кратные 14:____________________ 4) Кратные 60:
- Запишите все двузначные числа, кратные 17.
Ответ: ______________________________________
- Запишите все трёхзначные числа, кратные 115. Ответ: __________________________________
- Укажите какое-либо число, являющееся делителем каждого из чисел:
1)15 и 35; 2) 18 и 24; 3) 30 и 50; 4) 11 и 33.
Ответ: 1) __________; 2) __________; 3) __________; 4) __________.
- Укажите какое-либо число, кратное каждому из чисел:
1)3 и 7; 2) 4 и 8; 3) 6 и 8; 4) 12 и 18.
Ответ: 1)__________; 2)___________; 3) __________; 4) __________.
- Запишите все значения х, являющиеся делителями числа 78, при которых верно неравенство 6 < х < 38.
Ответ: _______________________________________
- Запишите все значения х, кратные числу 7, при которых верно неравенство 22 < х < 40.
Ответ: __________
- При делении числа а на 8 получили остаток 6. Какому условию должно удовлетворять число b, чтобы сумма а + b была кратна 8?
Ответ: __________
- Укажите, верно ли утверждение.
| Утверждение | Да/Нет |
| Если сумма делится нацело на число а, то каждое слагаемое делится нацело на число а | |
| Если один из множителей делится нацело на число а, то произведение делится нацело на число а | |
| Если ни один из множителей не делится нацело на число а, то произведение не делится нацело на число а |
- Встретились семеро друзей и пожали каждый друг другу руку. Сколько всего было рукопожатий?
§ 2. Признаки делимости на 10. на 5 и на 2
Повторяем теорию
- Заполните пропуски.
1) Если запись натурального числа оканчивается цифрой ____, то оно делится нацело на 10.
2) Если запись натурального числа оканчивается ____________цифрой, отличной от _____, то число не делится нацело на 10.
3) Если натуральное число разделить на 10, то остаток будет равен числу, записанному ___________ __________________
4) Натуральные числа, которые _______________________ называют чётными.
5) Натуральные числа, которые не делятся нацело на 2, называют __________
6) Цифры ______________________ называют чётными, а цифры ______________________— нечётными.
7) Если запись натурального числа оканчивается______________________________, то это число делится нацело на 2.
8) Если запись натурального числа оканчивается нечётной цифрой, то это число __________
9) Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на _________.
10) Если запись натурального числа оканчивается___________________________ отличной от____________________________________________________________________, то это число не делится нацело на 5.
Решаем задачи
- Из чисел 38, 469, 365, 740, 759, 4 535, 2 220, 3 170, 9 145, 12 618 делятся нацело:
1) на 10 —__________________________________________________________________
2) на 2 -___________________________________________________________________
3) на 5 —__________________________________________________________________-
- Поставьте в квадрате после каждого утверждения знак «+», если оно верно, или знак «-», если оно неверно.
1) Если число кратно 5, то оно кратно 10.
2) Если число кратно 10, то оно кратно 5.
3) Если число делится нацело на 2 и на 5, то оно делится нацело на 10.
- Запишите в порядке возрастания четыре первых нечётных двузначных числа, которые делятся нацело на 5.
Ответ: _________________________________________
- Запишите в порядке убывания три последних трёхзначных числа, которые кратны 10.
Ответ: _________________________________________
- Запишите все нечётные значения х, при которых верно неравенство 269 < х < 288.
Ответ: _________________________________________
- Запишите все значения х, кратные числу 5, при которых верно неравенство 169 < х < 195.
Ответ: _________________________________________
- Запишите все значения х, кратные числу 10, при которых верно неравенство 510 < х < 593.
Ответ: _________________________________________
- Не повторяя цифры в записи числа, запишите наибольшее:
1) пятизначное число, кратное 10;
2) шестизначное число, кратное 5;
3) семизначное число, кратное 2.
Ответ: 1)_______________; 2)________________; 3)______________
- Запишите все четырёхзначные числа, кратные числу 5, для записи которых используют цифры 2, 0, 5, 6 (цифры в записи числа не могут повторяться).
Ответ: __________
- Найдите наибольшее двузначное число а, при котором значение выражения а — 43 делится нацело на 5.
- Найдите наименьшее трёхзначное число b, при котором значение выражения 243 + b делится нацело на 10.
- Чётной или нечётной будет сумма девяти натуральных слагаемых, если:
1) шесть слагаемых чётные, а остальные — нечётные;
2) шесть слагаемых нечётные, а остальные — чётные?
Ответ: 1)_______________; 2)_______________
- Делится ли нацело на 5 значение выражения 115 + 65?
Решение:
Ответ:
- Можно ли заплатить без сдачи 30 р. с помощью 9 монет по 1 р. и по 5 р.?
Решение:
Ответ:
§ 3. Признаки делимости на 9 и на 3
Повторяем теорию
- Заполните пропуски.
1) Если _______________ числа делится нацело на 9, то и само число _________________
2) Если сумма цифр числа не делится нацело на 9, то и само число _________________
3) Если сумма цифр числа делится нацело на 3, то и _________________
4) Если _________________ числа _________________ нацело на 3, то и само число не делится нацело на 3.
Решаем задачи
- Заполните таблицу (поставьте знак «+» в случае утвердительного ответа или знак «—» в ином случае).
| Число | 2 736 | 6 438 | 1 443 | 5 665 | 7 417 | 2 412 | 8 910 |
| Кратно 9 | |||||||
| Кратно 3 | |||||||
| Кратно 2 и 3 |
- Заполните пропуски.
1) Наименьшим двузначным числом, которое делится нацело на 9, является число _________________
2) Наименьшим трёхзначным числом, которое делится нацело на 3, является число _________________
3) Наибольшим четырёхзначным числом, которое делится нацело на 9, является число ____________
4) Наименьшим числом, для записи которого использована только цифра 1 и которое делится нацело на 9, является число ___________________
- Какие из чисел 3 540, 2 601, 7 335, 6 228, 4 023, 5 949 делятся нацело на 3, но не делятся нацело ни на 2, ни на 5?
Ответ: _________________________ ____________________
- Запишите в квадрате одну из цифр 0, 7 или 5, чтобы получилось число, кратное 3.
1) 1 4__2; 2) 9__15.
- Запишите все значения а, кратные числу 9, при которых верно неравенство 134 < а < 152.
Ответ: _____________________________________________
- Запишите все значения b, кратные числу 3, при которых верно неравенство 234 < b < 252.
Ответ: _____________________________________________
- Из цифр 3, 4, 5, 6 составьте два различных трёхзначных числа, каждое из которых кратно 3, при этом в числе каждую из цифр используйте не более одного раза.
Ответ: ___________________________________________________
- Запишите в квадрате цифру, чтобы получилось число, кратное 9.
1) 8__3; 2) __55; 3)3 8__3; 4) 84__50.
- Какую цифру можно поставить вместо звёздочки, чтобы получилось число, кратное 3 (рассмотрите все возможные случаи): 1) 64 *58; 2) 73 6*2?
Ответ: ____________________________________________________
- Запишите наименьшее четырёхзначное число, которое делится нацело:
1) на 2 и на 3; 4) на 2 и на 9;
2) на 3 и на 5; 5) на 5 и на 9;
3) на 3 и на 10; 6) на 9 и на 10.
Ответ: 1) ________; 2) _________; 3) ________; 4) _________; 5) _________; 6)_________
- К числу 14 допишите слева и справа по одной цифре, чтобы получившееся число было кратно 15 (рассмотрите все возможные случаи).
Ответ: ________________________________________
- К числу 26 допишите слева и справа по одной цифре, чтобы получившееся число было кратно 45 (рассмотрите все возможные случаи).
Ответ: _________________________________________
- Запишите трёхзначное число, первая цифра которого 1, делящееся нацело на 9 и на 5, но не делящееся нацело на 2.
Ответ: __________________________________________
- Запишите трёхзначное число, первая цифра которого 5, делящееся нацело на 9, на 5 и на 2.
Ответ: ___________________________________________
- Делится ли нацело на 3 значение выражения: 1) 1014 – 1; 2) 1010 + 5?
Ответ: 1) _________________ 2) _________________
- В семье четыре сына. У каждого — одна сестра. Сколько всего детей в семье?
Ответ: _________________________________________
§ 4. Простые и составные числа
Повторяем теорию
- Заполните пропуски.
1) Натуральное число называют_____________________ если оно имеет только два натуральных делителя:________________________________
2) Наименьшим простым числом является число ______
3) Натуральное число называют____________________ если оно имеет больше двух натуральных делителей.
4) Число 1 не относят ни к ____________, ни к ________________ числам.
5) Любое составное число можно представить в виде произведения _________________, т. е. _________________ на простые множители.
- Подчеркните числа, которые являются простыми: 2, 5, 8, 11, 16, 17, 20, 26, 27, 30, 31, 32, 37, 39.
- Запишите все делители данного числа и обведите те из них, которые являются простыми числами:
1) делители 14; 2) делители 19; 3) делители 60.
Ответ: 1) __________________; 2) ________________-; 3) ________________
- Запишите натуральное число в виде произведения простых множителей.
1) 14=________________ 4)40 =_________________________
2) 20 =_______________ 5) 55 =________________________
3) 38 =_______________ 6) 78 =________________________
- Разложите число на простые множители:
- Поставьте в квадрате после каждого утверждения знак «+», если оно верно, или знак «—», если оно неверно.
1) Каждое натуральное число является или простым, или составным.
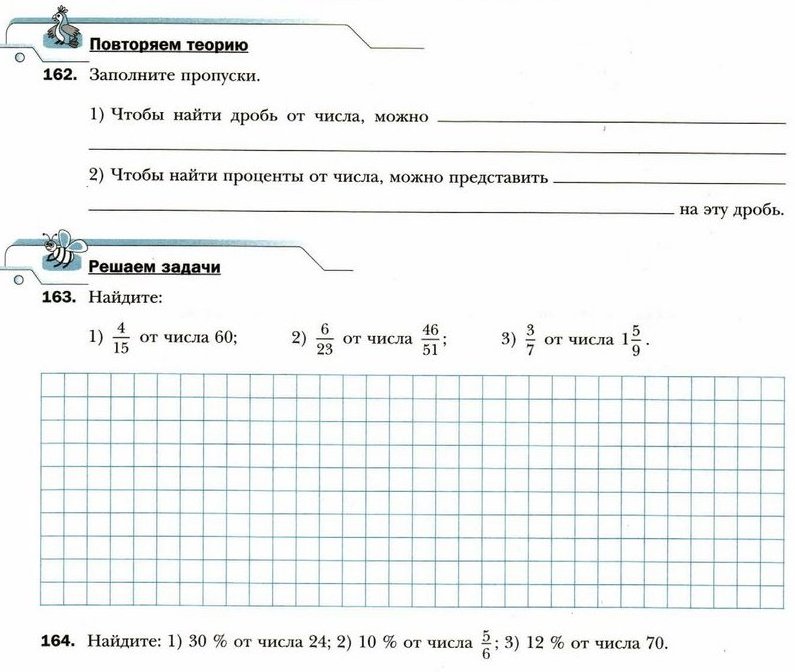
2) Если натуральное число не является простым, то оно составное.
3) Если натуральное число не является простым и оно больше 1, то оно составное.
4) Каждое чётное число является составным.
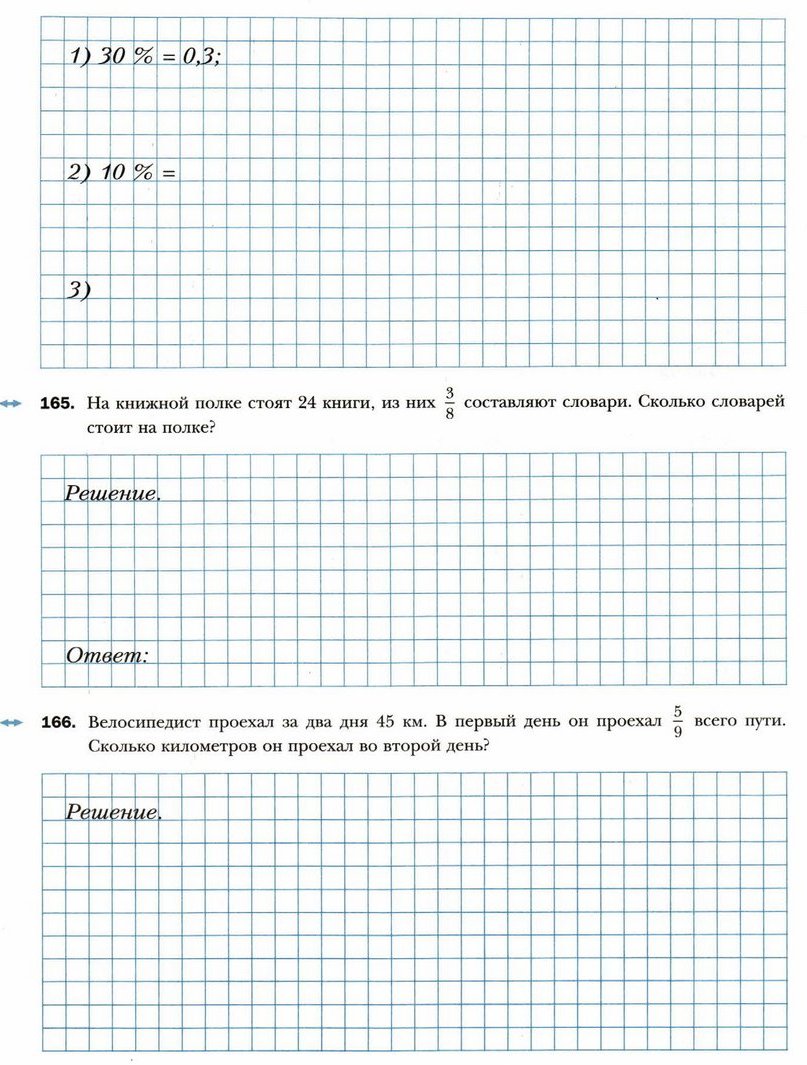
- Запишите все простые числа, которые больше 21 и меньше 42.
Ответ: _____________________________________________
- Запишите все составные числа, которые больше 50 и меньше 68.
Ответ: _____________________________________________
- Простым или составным числом будет произведение (поставьте знак «+» в соответствующей графе таблицы)?
| Произведение | 17 • 1 | 6 • 7 | 11 • 23 | 1 • 39 | 1 • 79 |
| Простое | |||||
| Составное |
- Запишите все делители числа, равного произведению 2 • 2 • 3 • 17
Ответ:
- Найдите частное от деления числа а на число b, если:
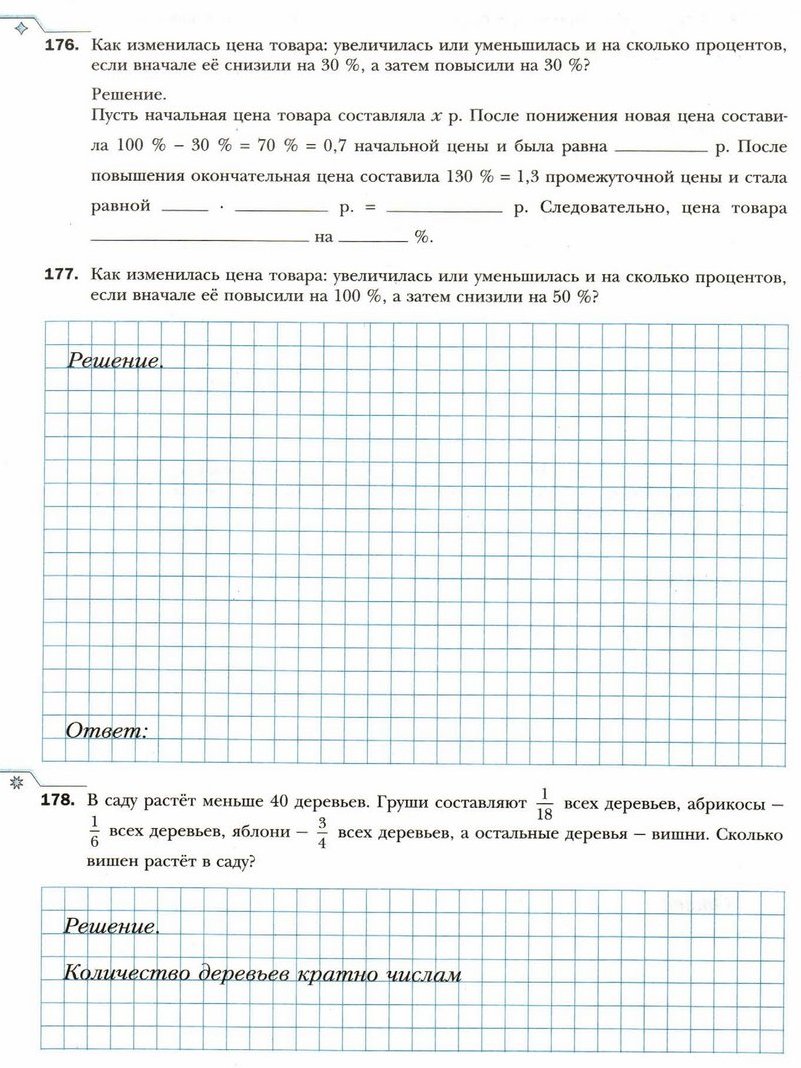
1) a = 2 • 3 • 3 • 3 • 19, b = 2 • 3 • 3 • 19;
2) а = 2 • 5 • 5 • 7 • 11 • 13, b = 5 • 7 • 13.
Ответ: 1) ______________; 2) ______________
- Мальчики собрали 145 грибов, причём каждый из них собрал одно и то же количество грибов. Сколько всего было мальчиков и сколько грибов собрал каждый из них?
Решение
Ответ
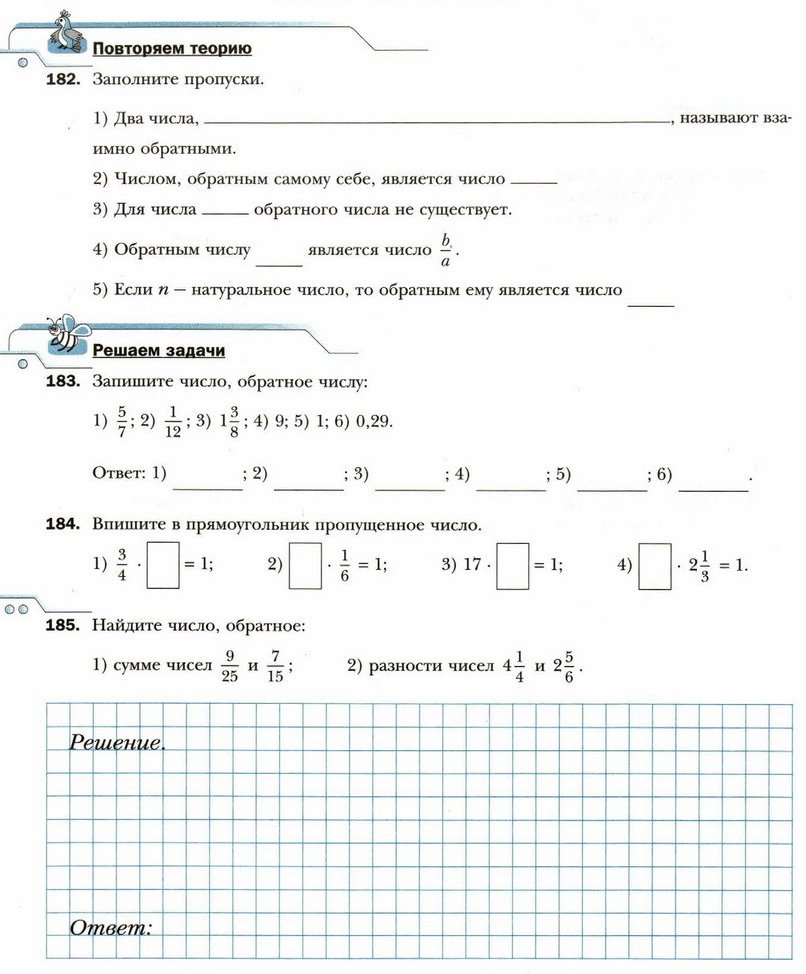
§ 5. Наибольший общий делитель
Повторяем теорию
- Заполните пропуски.
1) Наибольшее натуральное число, на которое__________________ _______________________ натуральных чисел, называют наибольшим общим делителем этих чисел.
2) Наибольший общий делитель чисел а и b обозначают так: ____________
3) Если наибольший общий делитель двух натуральных чисел____________, то их называют взаимно простыми.
4) Любые два ________________________ являются взаимно простыми.
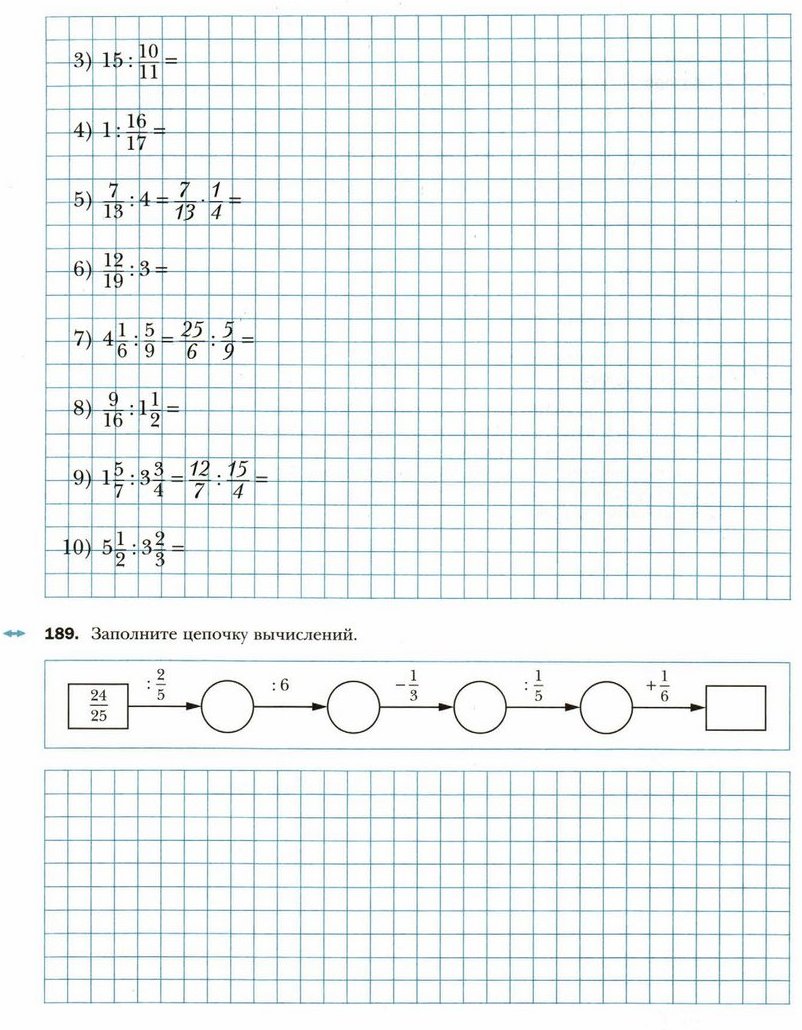
5) Если число а —______________числа b, то НОД (а; b) = а.
- Найдите наибольший общий делитель.
1) НОД (6; 15) =______________ 4) НОД (14; 28) = _
2) НОД (18; 24) =_____________ 5) НОД (8; 15) = —
3) НОД (24; 40) =_____________ 6) НОД (120; 150) =
- Найдите наибольший общий делитель чисел а и b, если:
1) а = 22 • З3 • 5 • 7 • 17, b = 23 • З2 • 5 • 11 • 19;
2) а = 25 • З2 • 73 • 13 • 232, b = З5 • 7 • 132 • 23.
Решение
Ответ
- Найдите наибольший общий делитель данных чисел, разложив их предварительно на простые множители:
1) 588 и 630; 3) 2 295 и 408;
2) 264 и 396; 4) 1 092 и 2 574.
Решение
Ответ
Решаем задачи
- Составьте все пары взаимно простых чисел из чисел 14, 15, 39 и 56.
Ответ: ___________________________________________
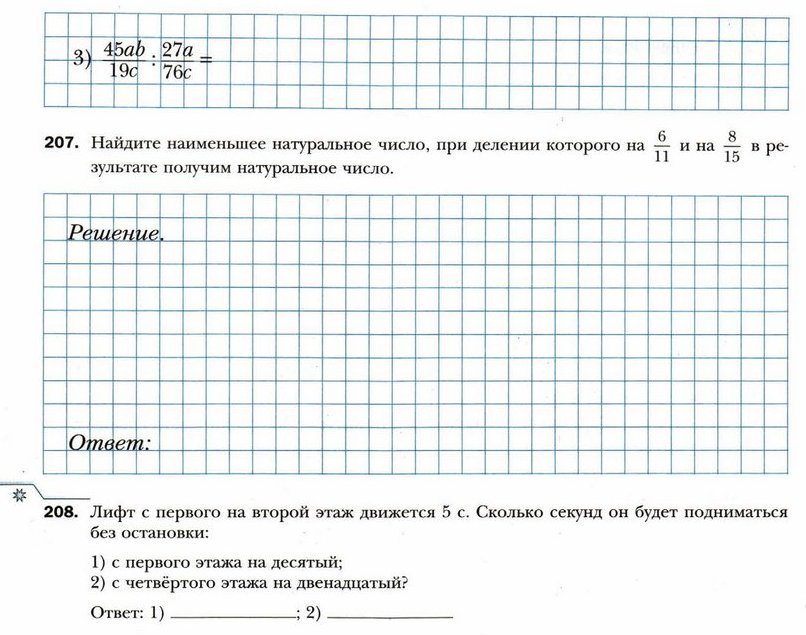
- К числу 48 подберите какое-либо однозначное число х, чтобы числа 48 и х были взаимно простыми.
Ответ: ___________________________________________
- Запишите какие-либо три пары чисел, наибольший общий делитель которых равен 6.
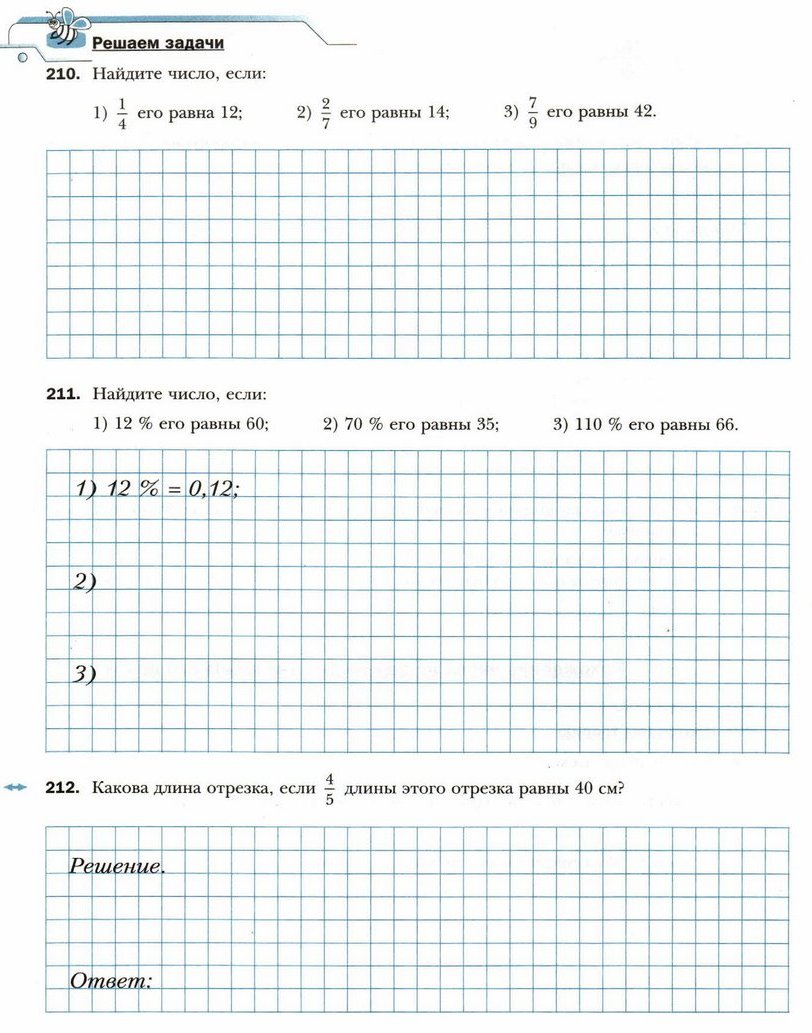
Ответ: ___________________________________________
- Запишите все правильные дроби со знаменателем 12, у которых числитель и знаменатель — взаимно простые числа.
Ответ: ___________________________________________
- Запишите все неправильные дроби с числителем 20, у которых числитель и знаменатель — взаимно простые числа.
Ответ: ______________
- Докажите, что числа 260 и 693 — взаимно простые.
- Докажите, что числа 136 и 255 не являются взаимно простыми.
- Для подарков первоклассникам приобрели 60 ручек, 84 фломастера и 108 цветных карандашей. Какое наибольшее количество одинаковых подарков можно из них составить, если необходимо использовать все приобретённые предметы?
- В коробке лежат 10 белых и 5 красных шаров. Какое наименьшее количество шаров надо наугад вынуть из коробки, чтобы среди них было 2 шара:
1) белых; 2) красных; 3) разного цвета; 4) одного цвета?
Ответ: 1) ________; 2) _______; 3) ________; 4) _________
§ 6. Наименьшее общее кратное
Повторяем теорию
- Заполните пропуски.
1) Наименьшее натуральное число, которое _______________________ __________________ натуральных чисел, называют наименьшим общим кратных этих чисел.
2) Наименьшее общее кратное чисел а и b обозначают так: ______
3) Если число а —_________________числа b, то НОК (а; b) = b.
4) Наименьшее общее кратное взаимно простых чисел равно _____
Решаем задачи
- Найдите наименьшее общее кратное.
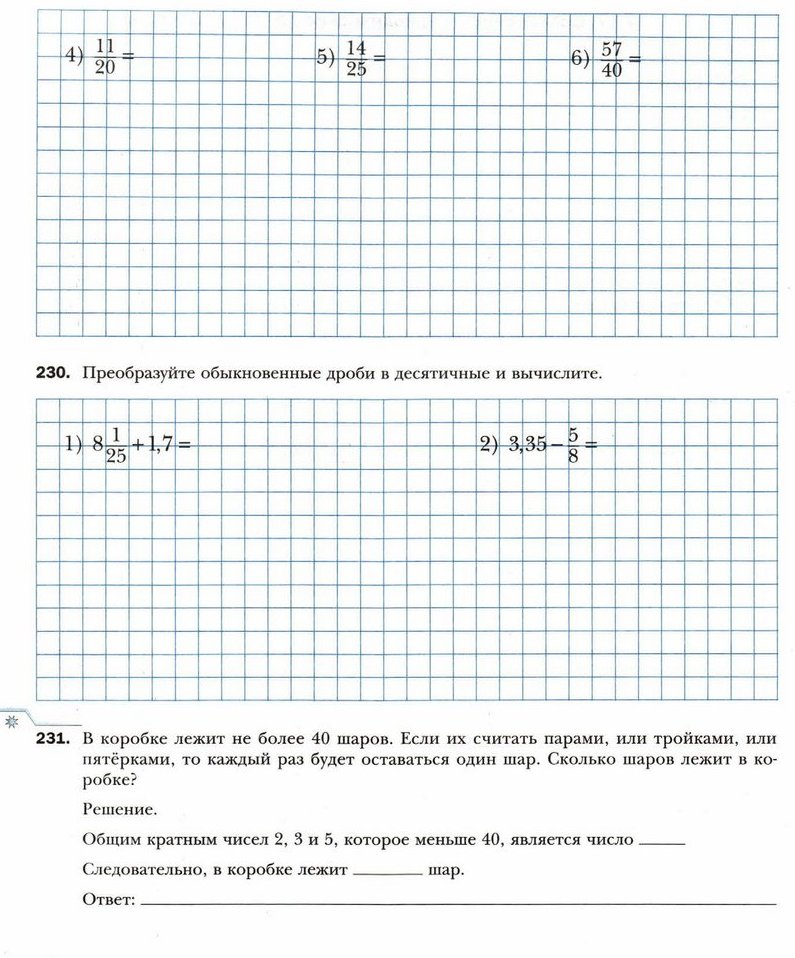
1) НОК (6; 9) =________ 4) НОК (70; 10) =
2) НОК (8; 10) =_______ 5) НОК (7; 8) = _
3) НОК (7; 14) =_______ 6) НОК (6; 25) = _
- Найдите наименьшее общее кратное чисел а и b, если: 1) а = 2 • З2 • 5, b = 2 • З3 • 7;
- Найдите наименьшее общее кратное данных чисел, разложив их предварительно на простые множители: 1) 56 и 84; 2) 72 и 90.
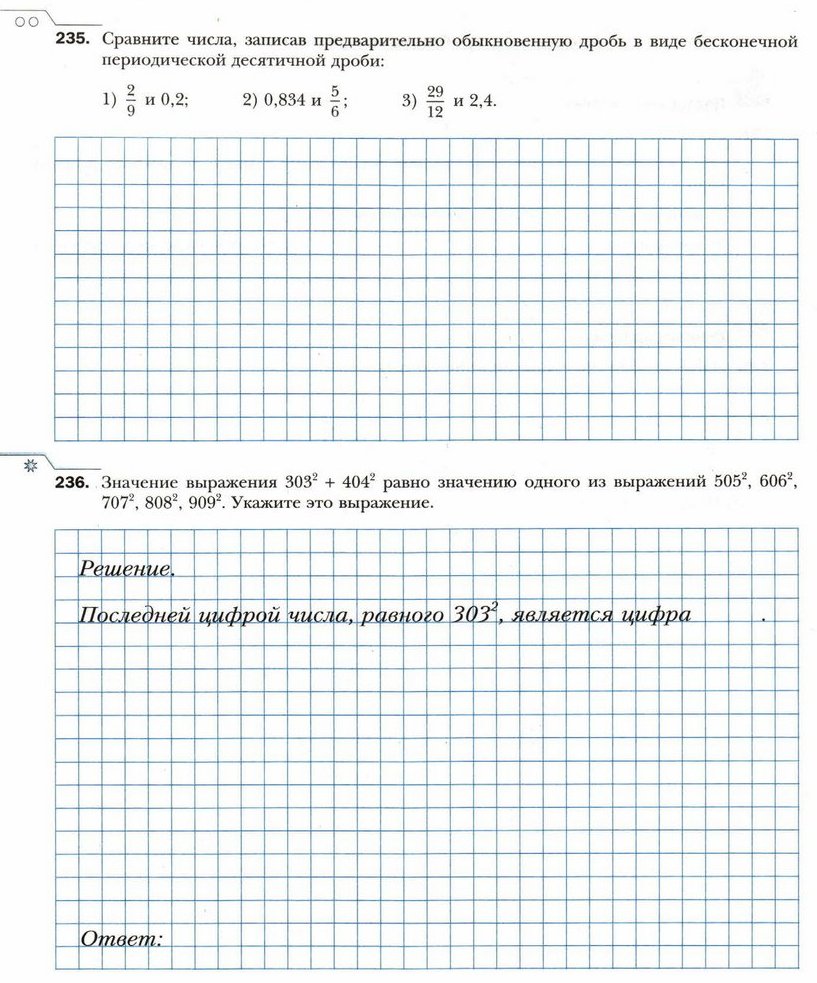
- Найдите наименьшее общее кратное знаменателей дробей:
- Запишите какие-либо три пары чисел, наименьшее общее кратное которых равно 72.
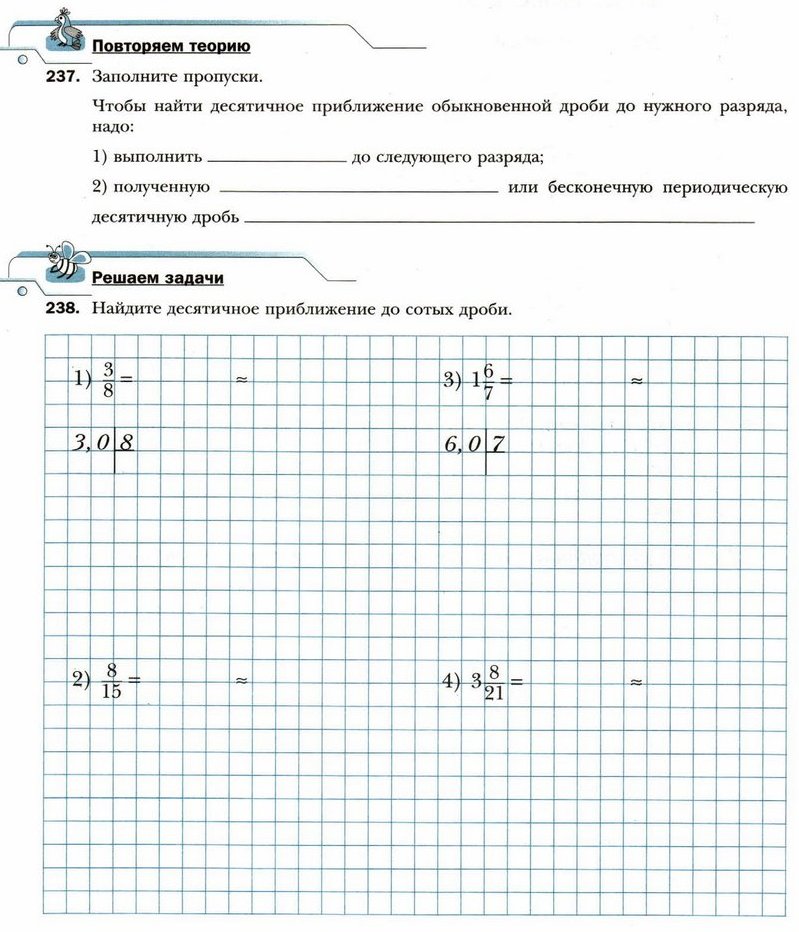
Ответ: _______________________________________________
- Найдите наименьшее общее кратное:
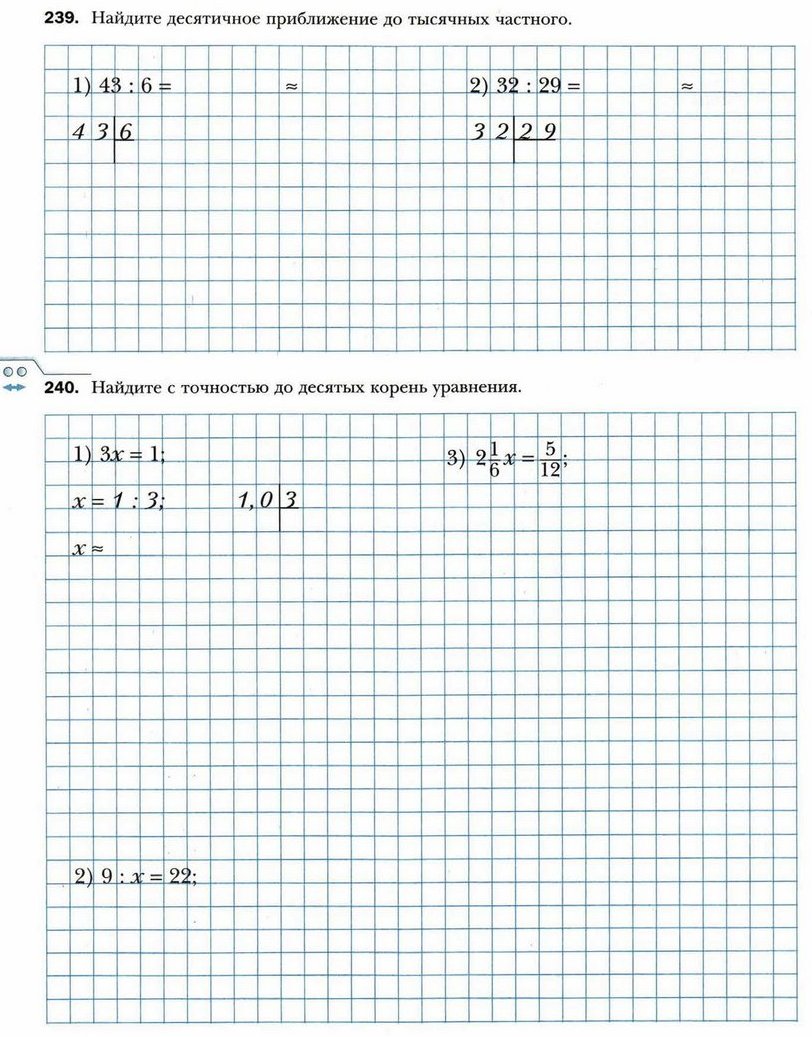
1) первых шести натуральных чисел;
2) первых шести чётных чисел;
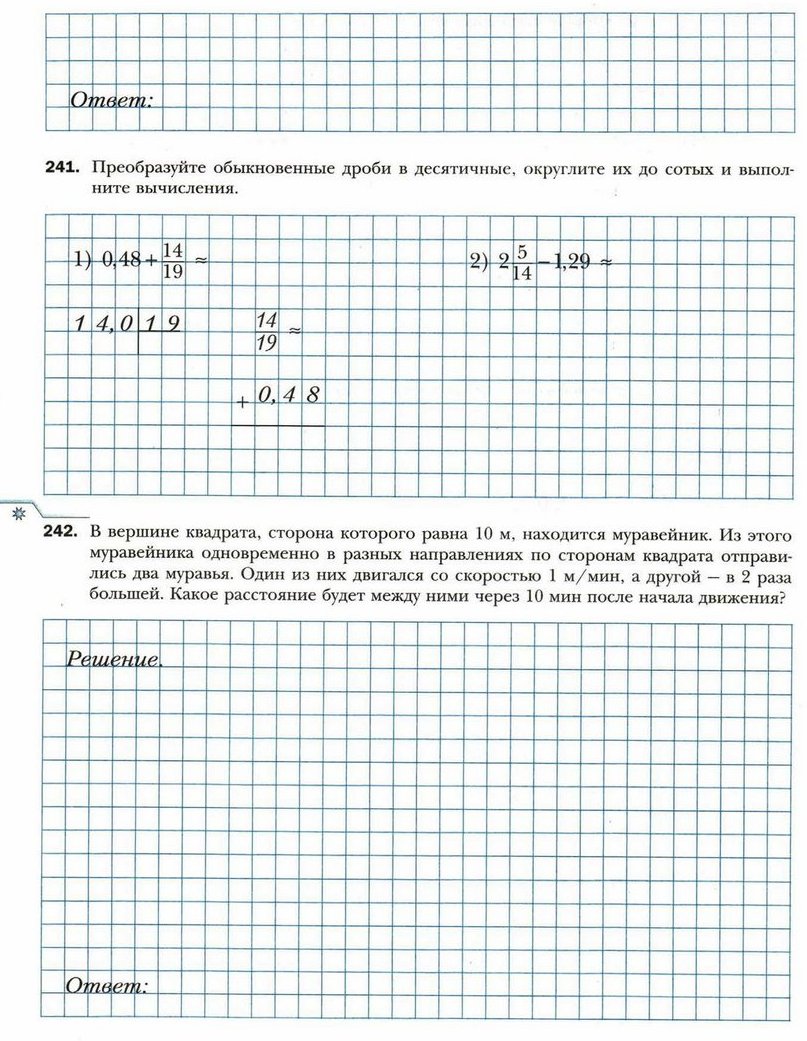
3) первых шести нечётных чисел;
4) первых шести составных чисел.
- Длина шага отца равна 80 см, а сына — 50 см. Какое наименьшее одинаковое расстояние должен пройти каждый из них, чтобы они оба сделали по целому числу шагов?
Решение
Ответ
- Петя ходит в компьютерный клуб один раз в 4 дня, Миша — в 5 дней, а Вася — в б дней. Они встретились в клубе в четверг. Через сколько дней и в какой день недели они встретятся в следующий раз?
- Две бригады цветоводов высадили одинаковое количество кустов роз. Первая бригада посадила розы по 18 кустов в ряд, а вторая — по 12 кустов. Сколько кустов посадила каждая бригада, если известно, что их было больше 100 и меньше 120?
- В каждый квадрат впишите по одной цифре, чтобы умножение полученных чисел было выполнено верно:
Глава 2. Обыкновенные дроби
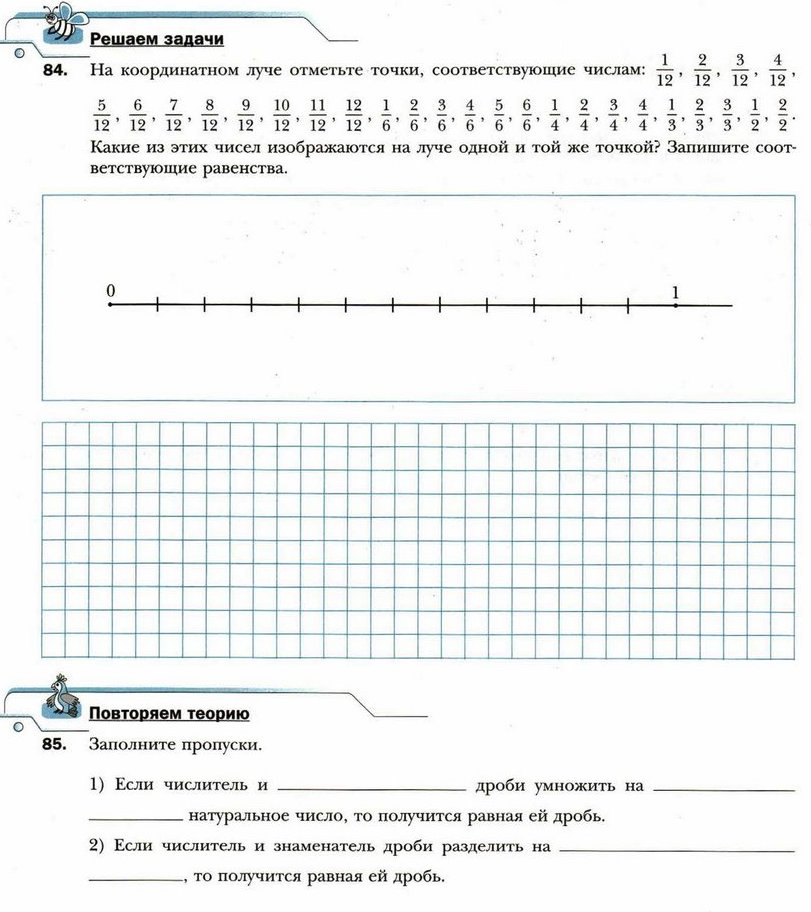
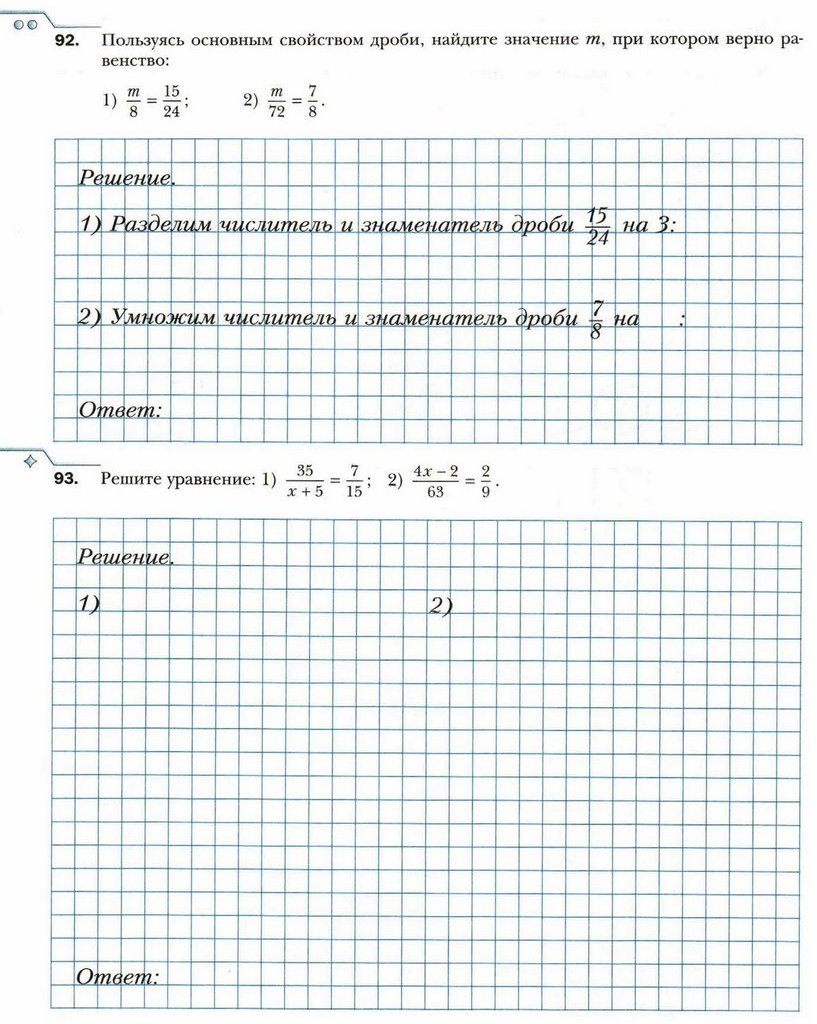
§ 7. Основное свойство дроби
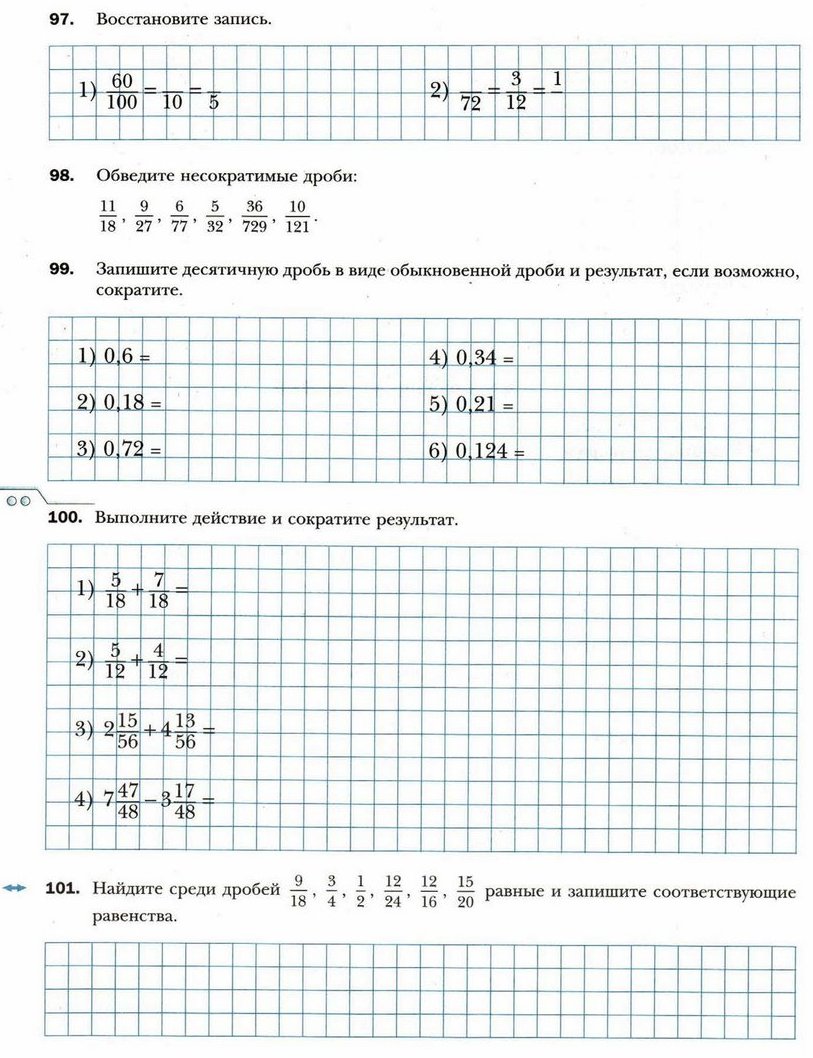
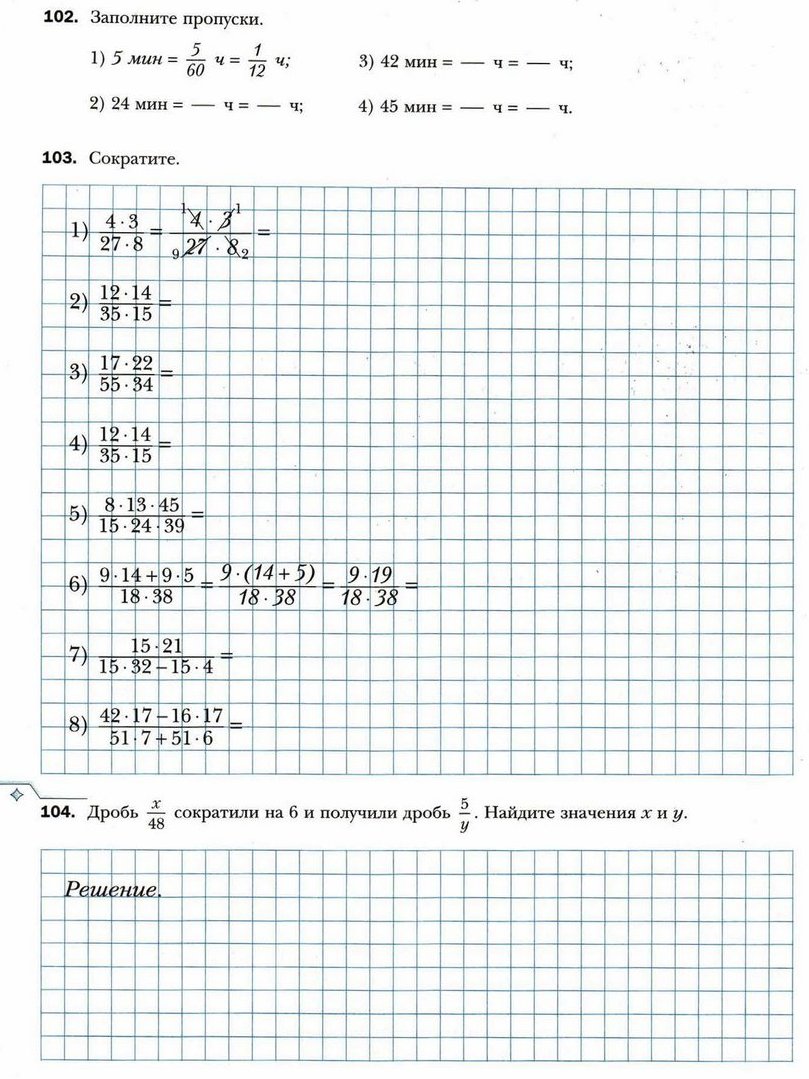
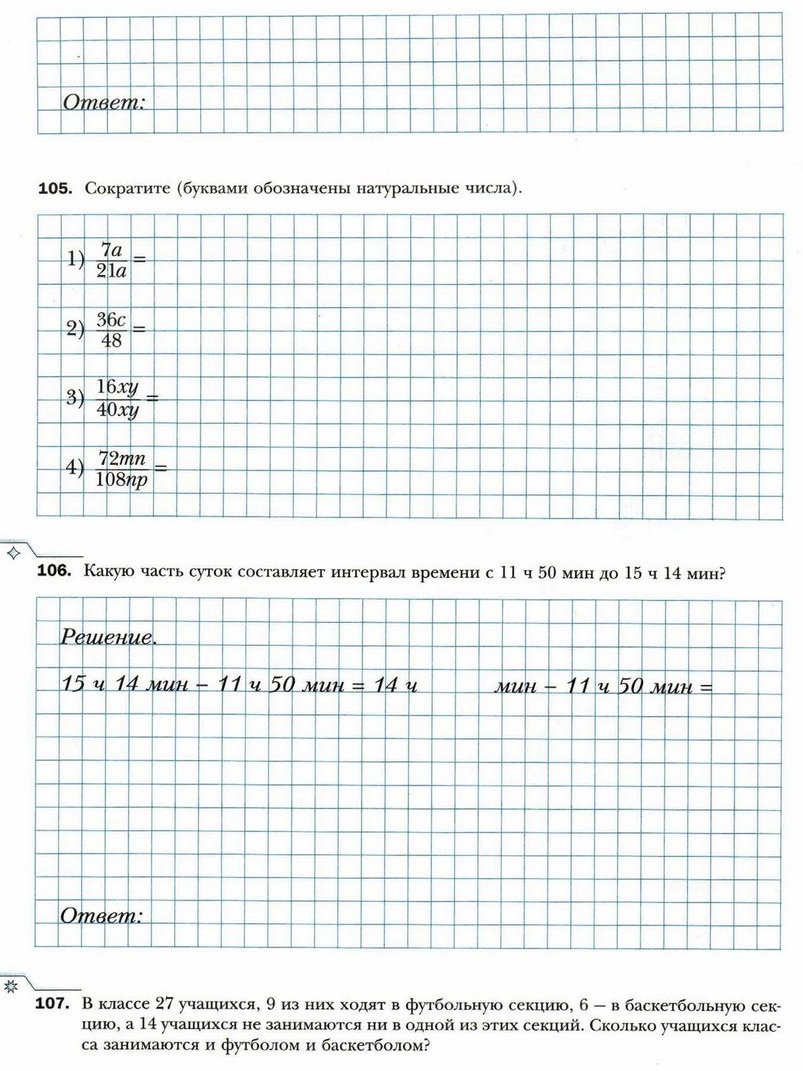
§ 8. Сокращение дробей
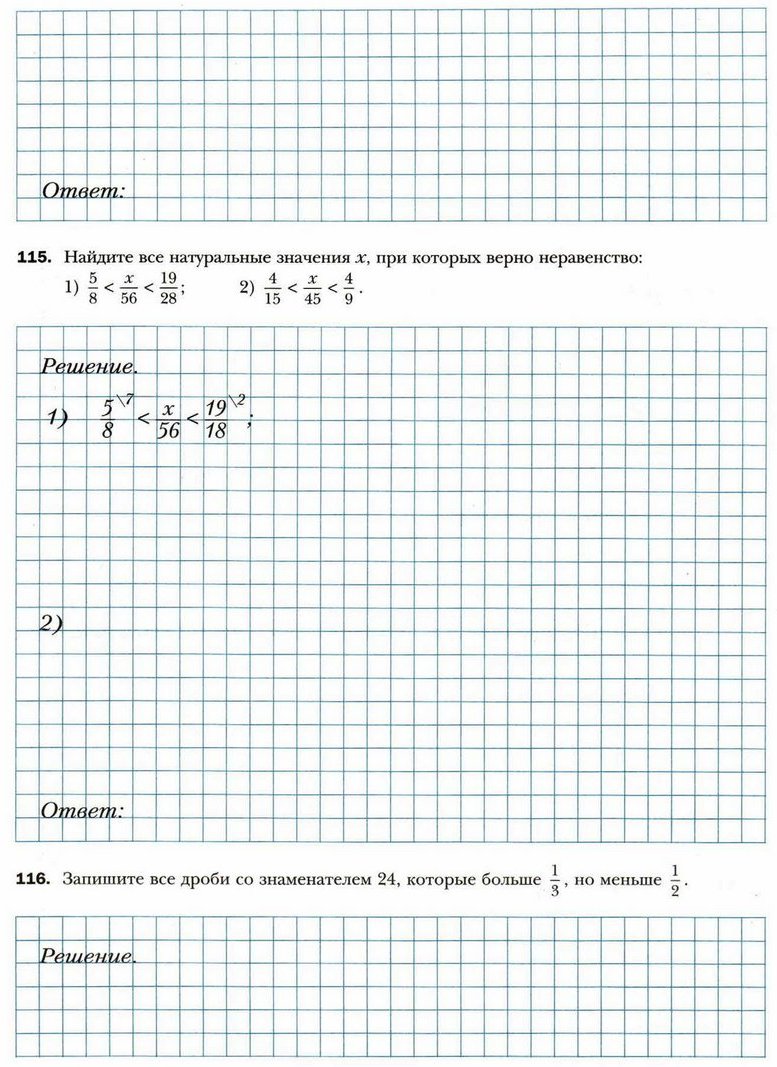
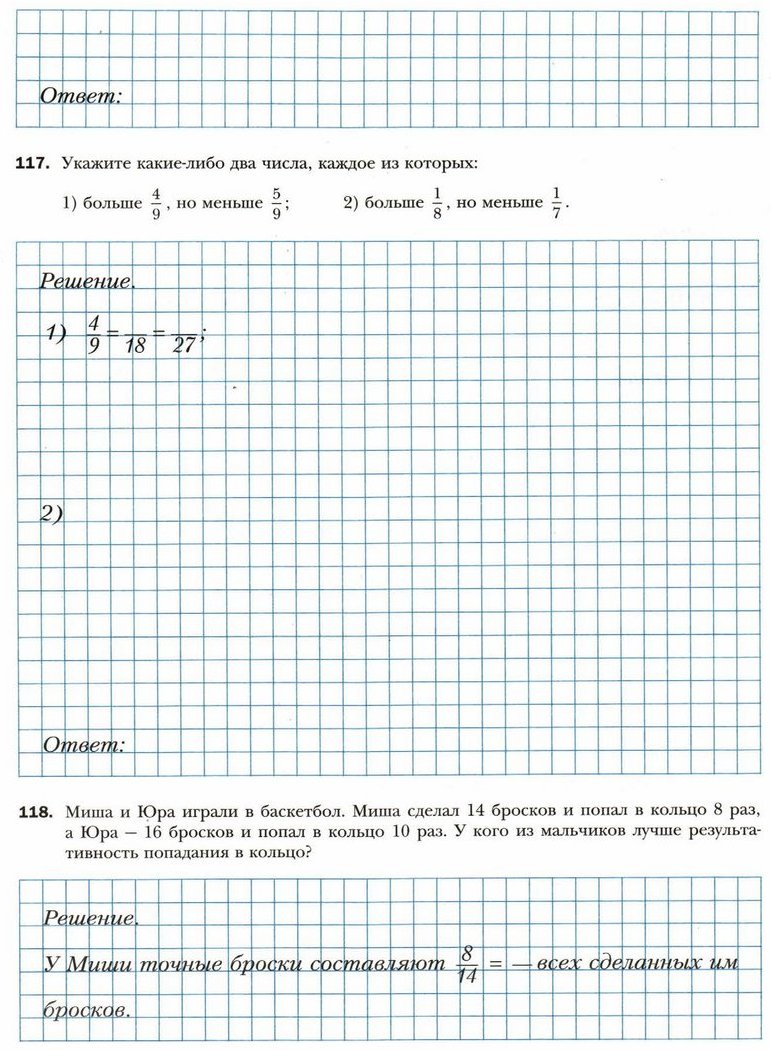
§ 9. Приведение дробей к общему знаменателю. Сравнение дробей
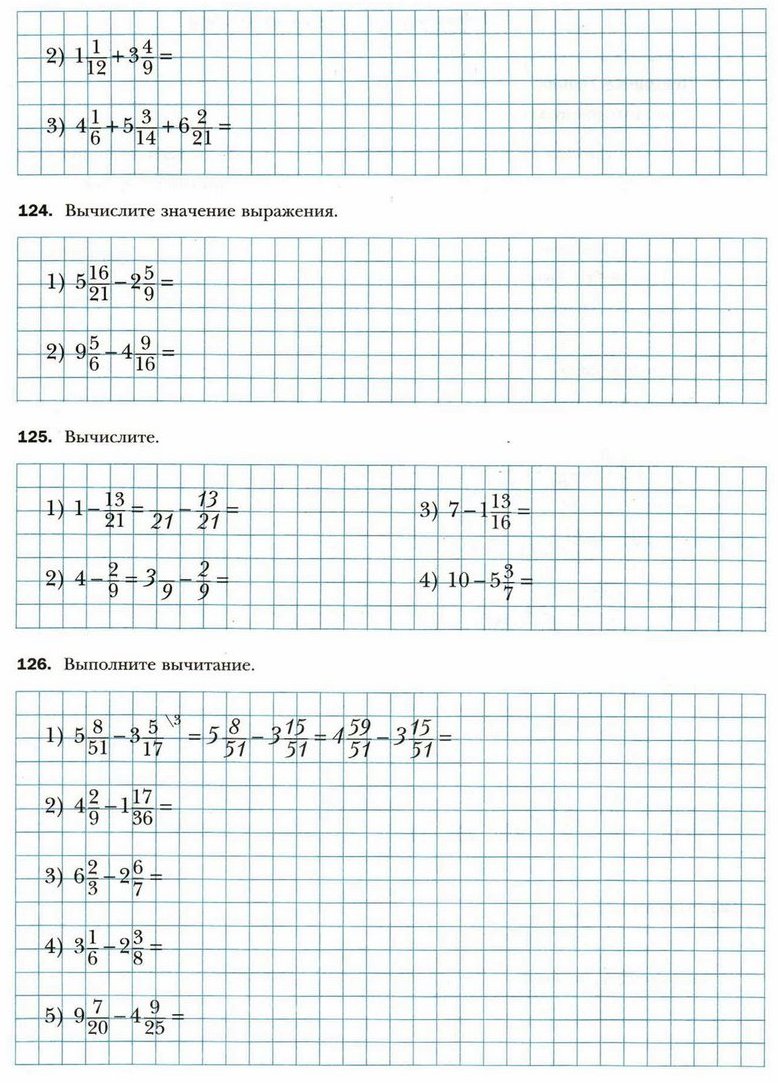
§ 10. Сложение и вычитание дробей
§ 11. Умножение дробей
§ 12. Нахождение дроби от числа
§ 13. Взаимно обратные числа
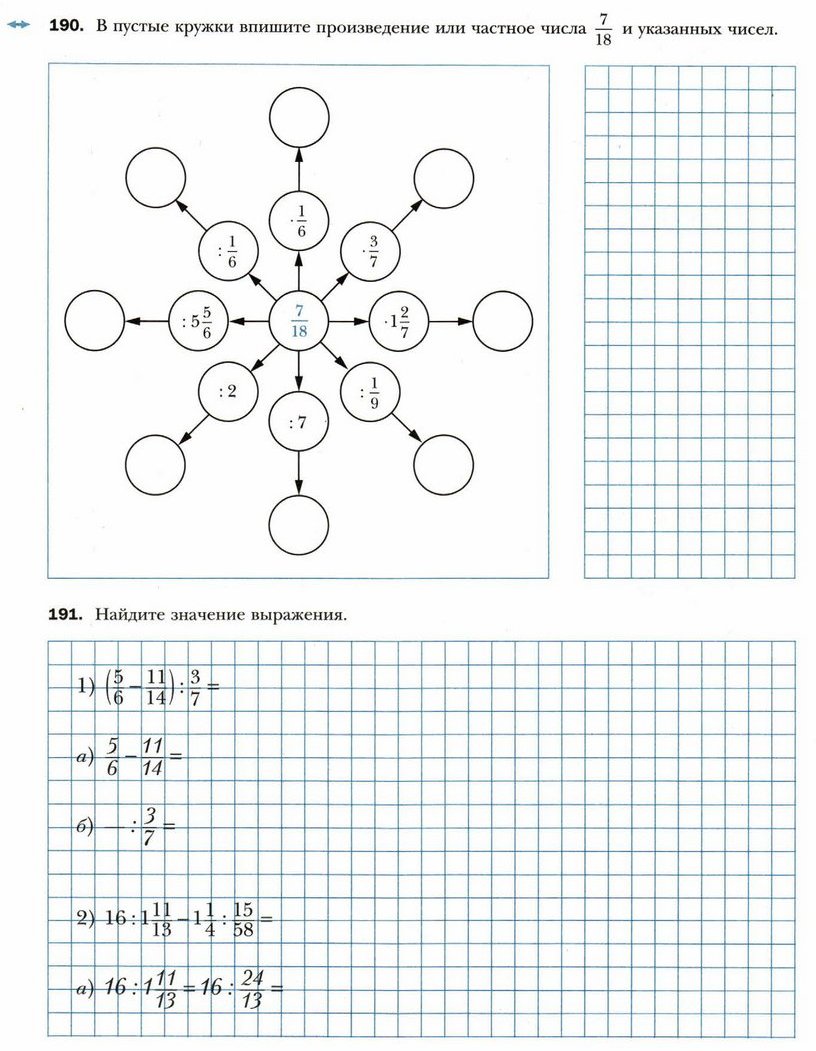
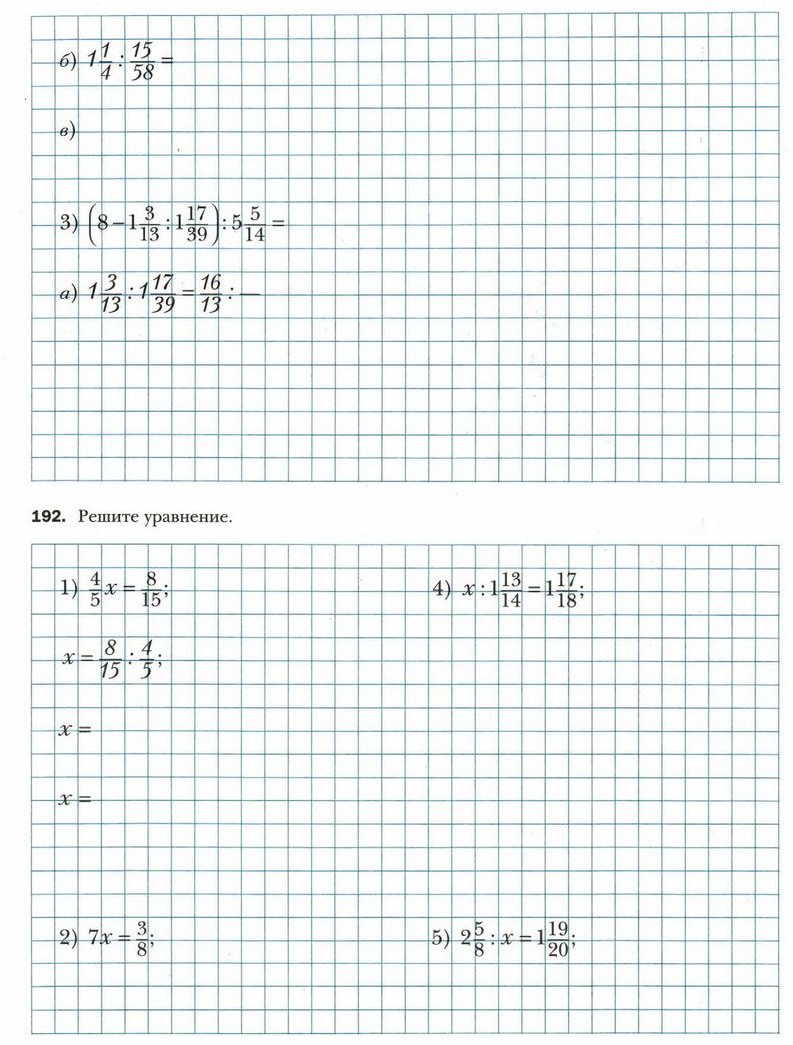
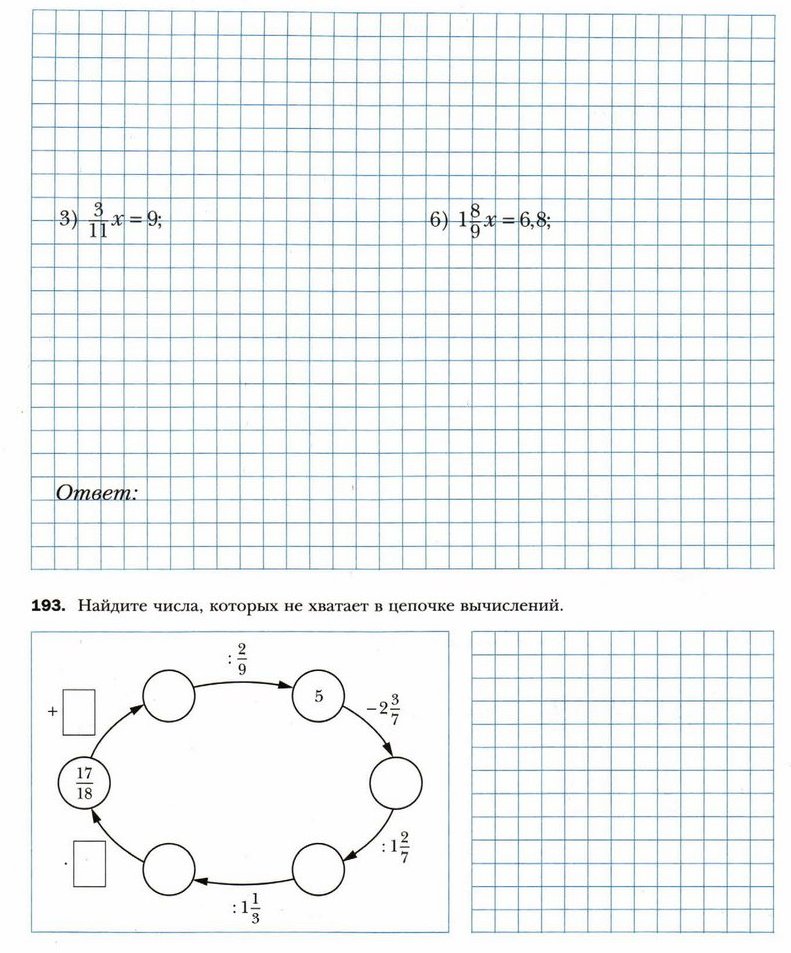
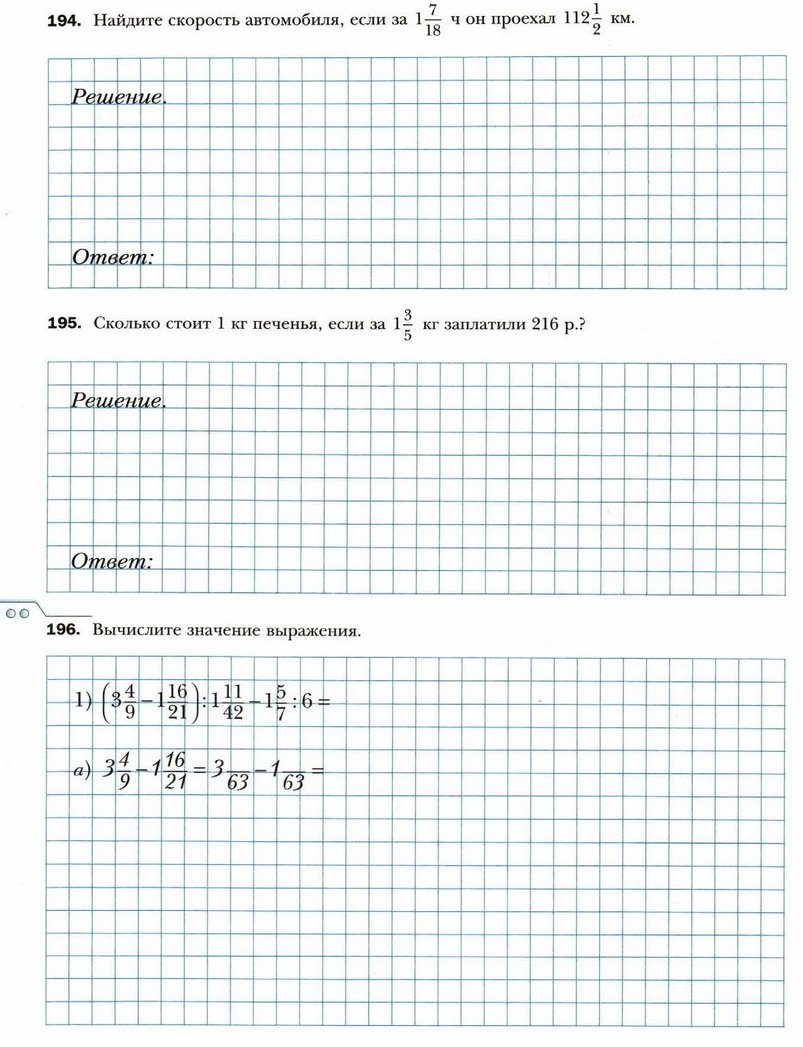
§ 14. Деление дробей
§ 15. Нахождение числа по заданному значению его дроби
§16. Преобразование обыкновенных дробей в десятичные

§ 17. Бесконечные периодические десятичные дроби

§ 18. Десятичное приближение обыкновенной дроби
Рабочая тетрадь № 1 по математике для 6 класса УМК Мерзляк, Полонский, Якир. Цитаты использованы в учебных целях. Мерзляк 6 Рабочая тетрадь 1.