Математика 6 класс УЧЕБНИК в 2-х частях (УМК Виленкин и др.) § 4. Отношения и пропорции (Отношения. Пропорции. Прямая и обратная пропорциональные зависимости. Масштаб. Длина окружности и площадь круга. Шар. Задания для самопроверки. Проектные задачи).
Ознакомительная версия перед покупкой. Цитаты из учебного пособия использованы в учебных целях.
Математика 6 класс (УМК Виленкин)
§ 4. Отношения и пропорции
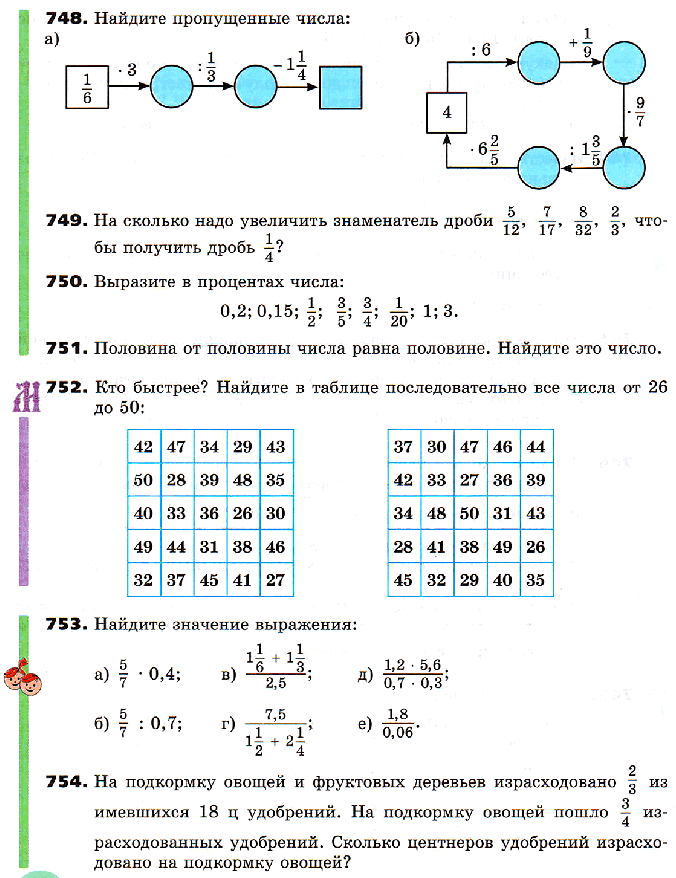
20. Отношения
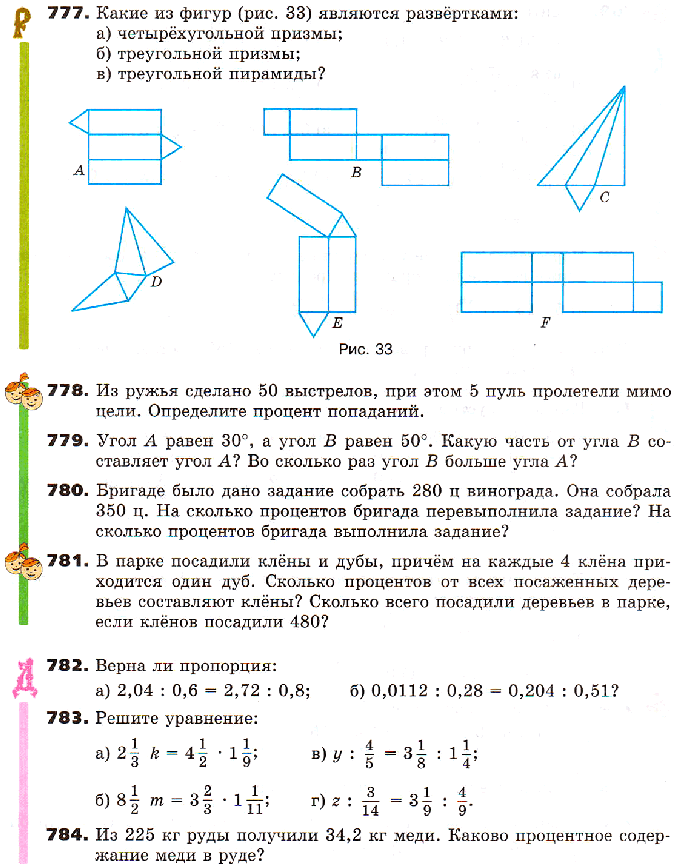
21. Пропорции
22. Прямая и обратная пропорциональные зависимости
Если станок с числовым программным управлением за 2 ч изготовляет 28 деталей, то за вдвое большее время, т. е. за 4 ч, он изготовит вдвое больше таких деталей, т. е. 28 • 2 = 56 деталей. Во сколько раз больше времени будет работать станок, во столько раз больше деталей он изготовит. Значит, равны отношения 4 : 2 и 56 : 28. Следовательно, верна пропорция 4 : 2 = 56 : 28. Такие величины, как время работы станка и число изготовленных деталей, называют прямо пропорциональными величинами.
Прямо пропорциональная зависимость
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Пусть путь из города А в город В поезд со скоростью 40 км/ч проходит за 12 ч. Если скорость движения увеличить вдвое, т. е. сделать её равной 80 км/ч, то на этот же путь поезд затратит вдвое меньше времени, т. е. 6 ч. Во сколько раз увеличится скорость движения, во столько же раз уменьшится время движения. В этом случае отношение 80 : 40 будет равно не отношению 6 : 12, а обратному отношению 12:6. Следовательно, верна пропорция 80 : 40 = = 12 : 6. Такие величины, как скорость и время, называют обратно пропорциональными величинами.
Обратно пропорциональная зависимость
Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.
Если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины.
Не всякие две величины являются прямо пропорциональными или обратно пропорциональными. Например, рост ребёнка увеличивается при увеличении его возраста, но эти величины не являются пропорциональными, так как при удвоении возраста рост ребёнка не удваивается.
Задачи на пропорциональные величины можно решить с помощью пропорции.
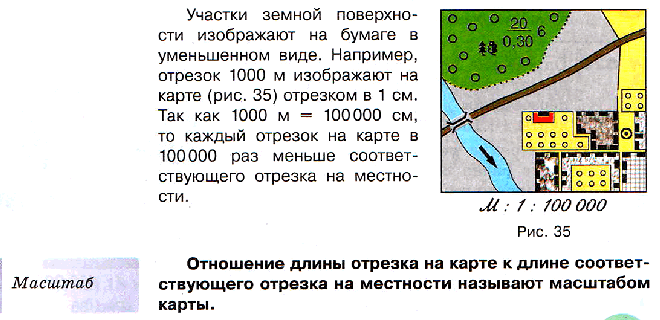
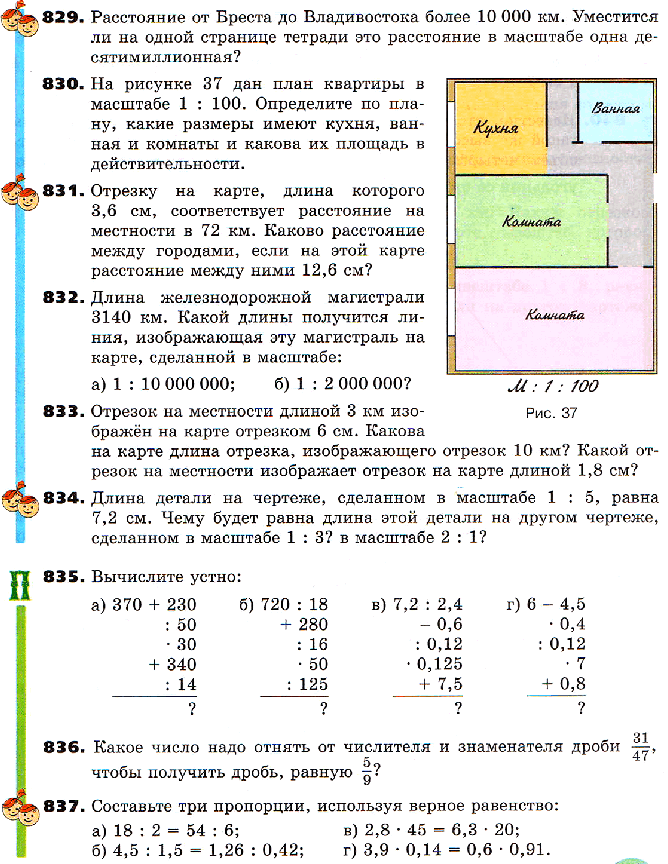
23. Масштаб
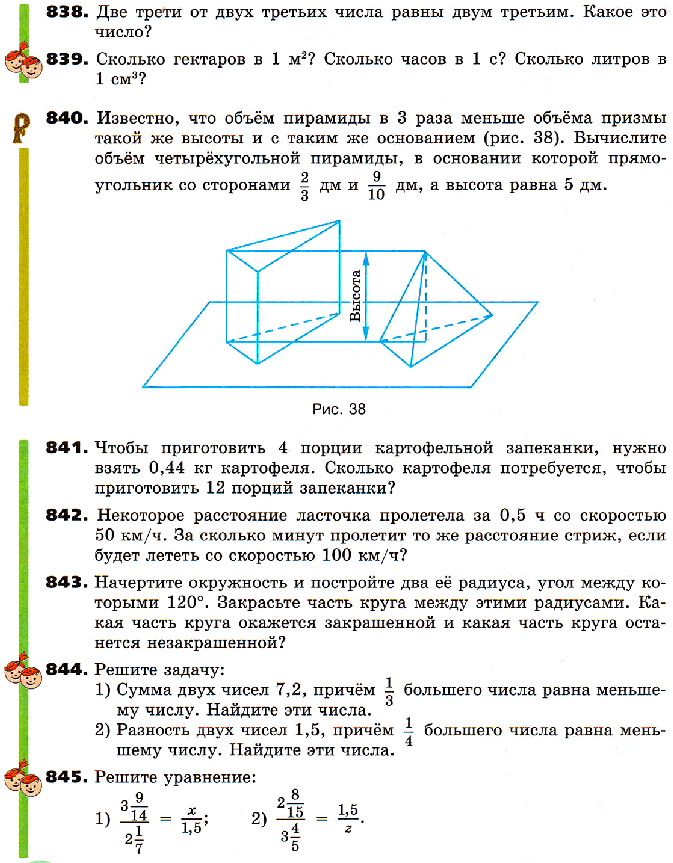
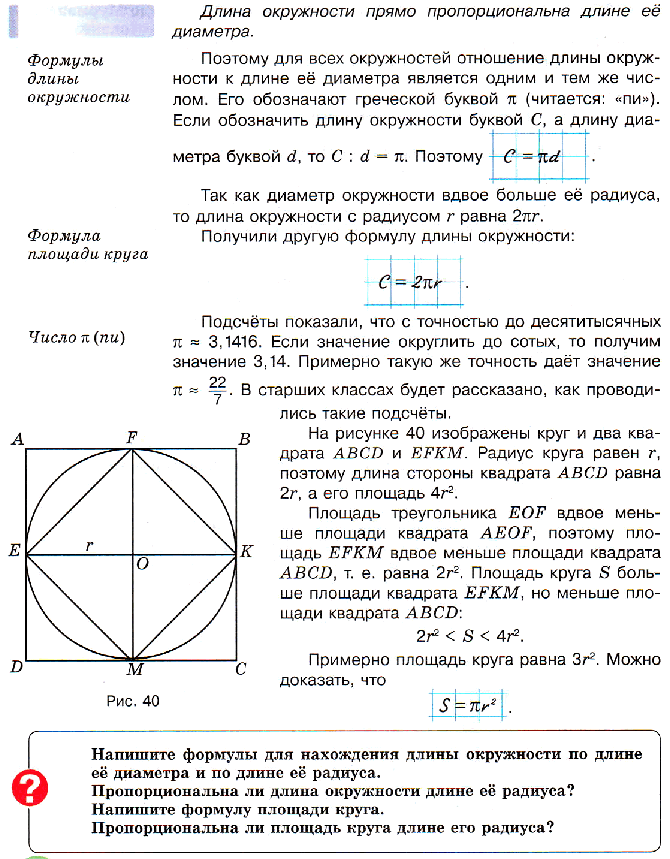
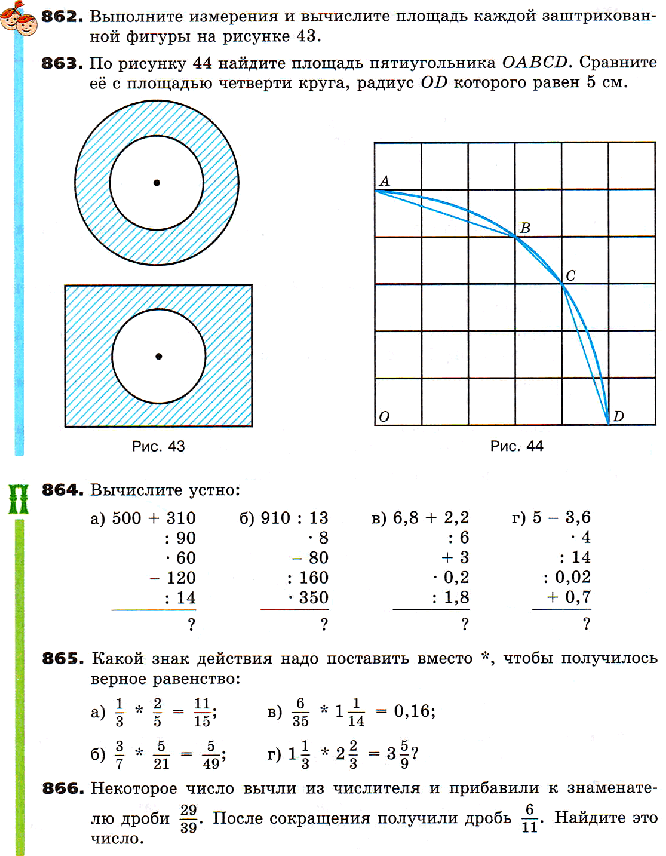
24. Длина окружности и площадь круга
25. Шар



Тесты для самопроверки

Проектные задачи
- Задача для будущего IT-конструктора.
Может ли существовать куб, длина ребра которого натуральное число, а площадь его развертки простое число? - Задача для будущего медика.
Фармацевт готовил микстуру от кашля. В качестве действующего вещества он использовал порошок из корня солодки (солодка — лекарственное растение). В мензурку с 10 %-м водным раствором солодки он добавил 5 граммов порошка. Получился 20 %-й раствор солодки. Сколько граммов действующего вещества стало в мензурке?
Вы смотрели: Математика 6 класс УЧЕБНИК в 2-х частях (УМК Виленкин и др.) § 4. Отношения и пропорции (Отношения. Пропорции. Прямая и обратная пропорциональные зависимости. Масштаб. Длина окружности и площадь круга. Шар. Задания для самопроверки. Проектные задачи).