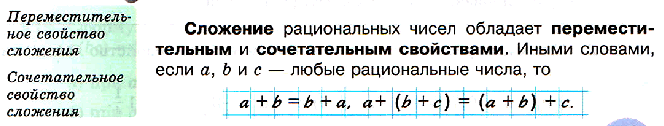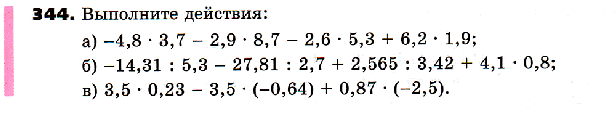Математика 6 класс УЧЕБНИК в 2-х частях (УМК Виленкин и др.) § 7. Умножение и деление положительных и отрицательных чисел (Умножение. Деление. Рациональные числа. Свойства действий с рациональными числами).
Ознакомительная версия перед покупкой. Цитаты из учебного пособия использованы в учебных целях. Математика 6 класс (УМК Виленкин)
§ 7. Умножение и деление
положительных и отрицательных чисел.
35. Умножение.
Задача 1. Фабрика выпускает в день 200 мужских костюмов. Когда стали выпускать костюмы нового фасона, расход ткани на один костюм изменился на +0,4 м2. На сколько изменился расход ткани на костюмы за день?
Решение. Расход ткани на каждый костюм увеличился на 0,4 м2. Поэтому, чтобы решить задачу, надо умножить 0,4 на 200. Получим 0,4 • 200 = 80. Значит, расход ткани на костюмы за день увеличился на 80 м2, иными словами, изменился на 80 м2.
Задача 2. Фабрика выпускает в день 200 мужских костюмов. Когда стали выпускать костюмы нового фасона, расход ткани на один костюм изменился на –0,4 м2. На сколько изменился расход ткани на костюмы за день?
Решение. Расход ткани на каждый костюм уменьшился на 0,4 м2. Поэтому расход ткани на костюмы за день уменьшился на 80 м2 (0,4 • 200 = 80). Это значит, что расход ткани на костюмы за день изменился на –80 м2.
Таким образом, произведение –0,4 и 200 равно –80, т. е. –0,4 • 200 = –(0,4 • 200) = –80.
Считают, что и 200 • (–0,4) = –(200 • 0,4) = –80.
◊ Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить перед полученным числом знак «–».
Например, (–1,2) • 0,3 = –(1,2 • 0,3) = –0,36;
1,2 • (–0,3) = –(1,2 • 0,3) = –0,36.
Сравнивая эти два произведения с произведением 1,2 • 0,3 = 0,36, можно заметить, что при изменении знака любого множителя знак произведения меняется, а его модуль остаётся тем же.
Если же меняются знаки обоих множителей, то произведение меняет знак дважды, и в результате знак произведения не меняется: 8 • 1,1 = 8,8; (–8) • 1,1 = –8,8; (–8) • (–1,1) = –(–8,8) = 8,8. Видим, что произведение отрицательных чисел есть число положительное.
◊ Чтобы перемножить два отрицательных числа, надо перемножить их модули.
Например, (–3,2) • (–9) = |–3,2| • |–9| = 3,2 • 9 = 28,8. Обычно пишут короче: (–3,2) • (–9) = 3,2 • 9 = 28,8. Так как (–3) • 2 = –(3 • 2), то можно первый множитель писать без скобок, т. е. (–3) • 2 = –3 • 2.
36. Деление.
37. Рациональные числа.
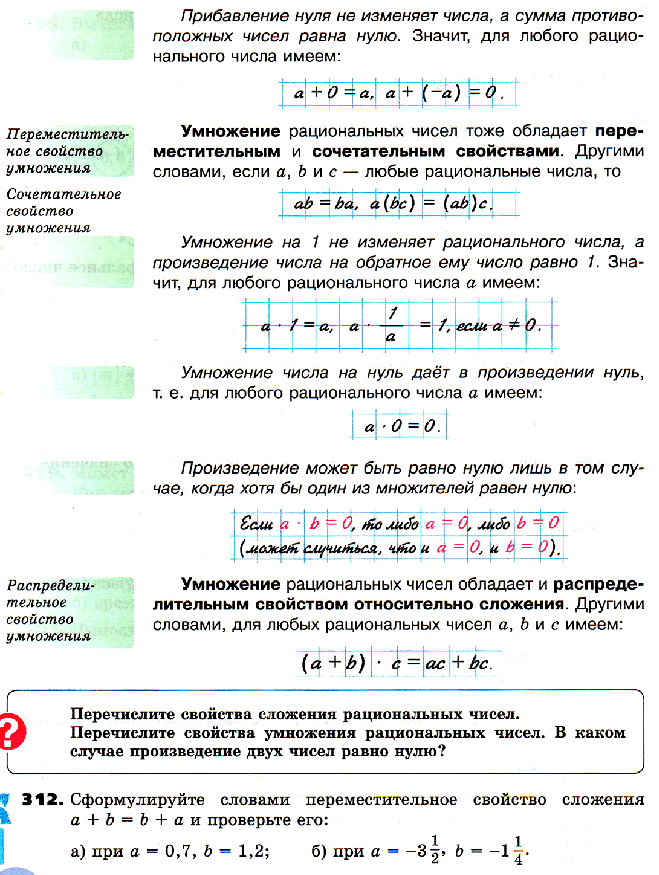
38. Свойства действий с рациональными числами.
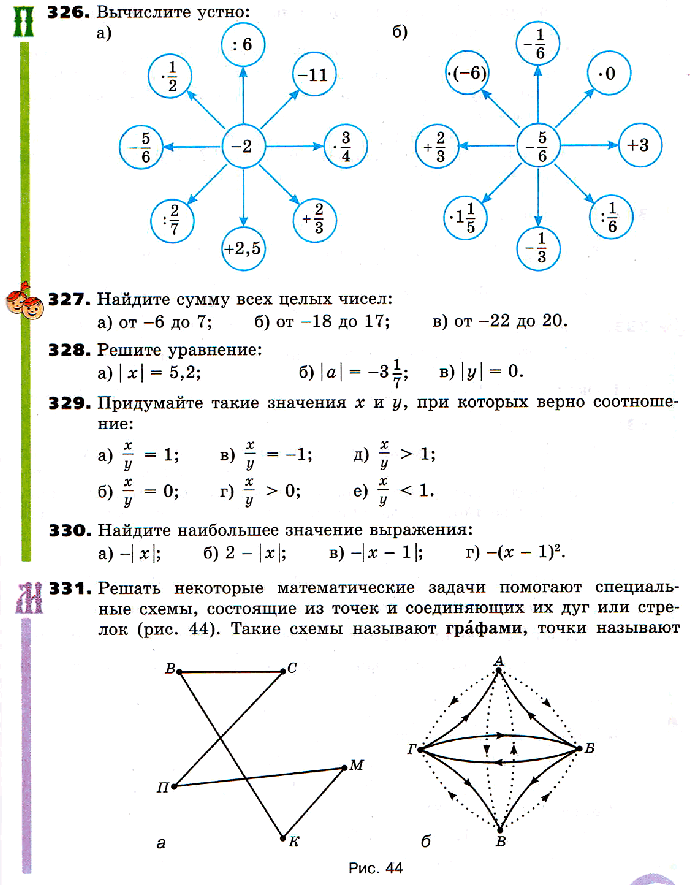
Задания для самопроверки

С рациональными числами люди, как вы знаете, знакомились постепенно. Вначале при счёте предметов возникли натуральные числа. На первых порах их было немного. Так, ещё недавно у туземцев островов в Торресовом проливе (отделяющем Новую Гвинею от Австралии) были в языке названия только двух чисел: «урапун» (один) и «оказа» (два). Островитяне считали так: «оказа–урапун» (три), «оказа–оказа» (четыре) и т. д. Все числа, начиная с семи, туземцы называли словом, обозначавшим «много».
Учёные полагают, что слово для обозначения сотни появилось более 7000 лет назад, для обозначения тысячи – 6000 лет назад, а 5000 лет тому назад в Древнем Египте и в Древнем Вавилоне появляются названия для громадных чисел – до миллиона. Но долгое время натуральный ряд чисел считался конечным: люди думали, что существует самое большое число.
Величайший древнегреческий математик и физик Архимед (287– 212 гг. до н. э.) придумал способ описания громадных чисел. Самое большое число, которое умел называть Архимед, было настолько велико, что для его цифровой записи понадобилась бы лента в две тысячи раз длиннее, чем расстояние от Земли до Солнца.
Но записывать такие громадные числа ещё не умели. Это стало возможным только после того, как индийскими математиками в VI в. была придумана цифра нуль и ею стали обозначать отсутствие единиц в разрядах десятичной записи числа.
При разделе добычи и в дальнейшем при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести «ломаные числа» – обыкновенные дроби. Действия над дробями ещё в Средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби».
Чтобы облегчить действия с дробями, были придуманы десятичные дроби. В Европе их ввёл в 1585 г. голландский математик и инженер Симон Стёвин.
Отрицательные числа появились позднее, чем дроби. Долгое время такие числа считали «несуществующими», «ложными» прежде всего из–за того, что принятое истолкование для положительных и отрицательных чисел «имущество – долг» приводило к недоумениям: можно сложить или вычесть «имущества» или «долги», но как понимать произведение или частное «имущества» и «долга»?
Однако, несмотря на такие сомнения и недоумения, правила умножения и деления положительных и отрицательных чисел были предложены в III в. греческим математиком Диофантом (в виде: «Вычитаемое, умноженное на прибавляемое, даёт вычитаемое; вычитаемое на вычитаемое даёт прибавляемое» и т. д.), а позже индийский математик Бхаскара (XII в.) выразил те же правила в понятиях «имущество», «долг» («Произведение двух имуществ или двух долгов есть имущество; произведение имущества и долга есть долг». То же правило и при делении).
Было установлено, что свойства действий над отрицательными числами те же, что и над положительными (например, сложение и умножение обладают переместительным свойством). И наконец с начала XIX в. отрицательные числа стали равноправными с положительными. а дальнейшем в математике появились новые числа – иррациональные, комплексные и другие. О них вы узнаете в старших классах.
Проектные задачи
- Задача для будущего геолога.
Придумайте свой шифр (или используйте известные примеры) и зашифруйте текст «Без труда не вынешь рыбку из пруда». - Задача для будущего дипломата.
Придумайте свой шифр (или используйте известные примеры) и зашифруйте текст «Победа в воздухе не вьется, а руками в труде достаётся».
Вы смотрели: Математика 6 класс УЧЕБНИК в 2-х частях (УМК Виленкин и др.) § 7. Умножение и деление положительных и отрицательных чисел (Умножение. Деление. Рациональные числа. Свойства действий с рациональными числами).