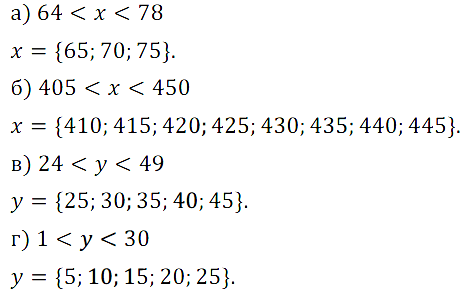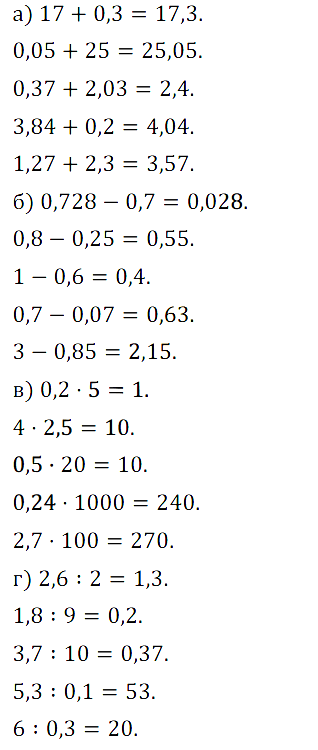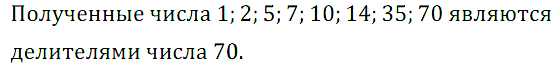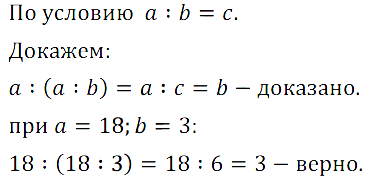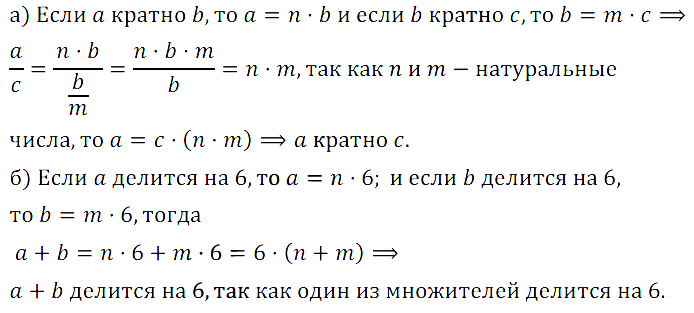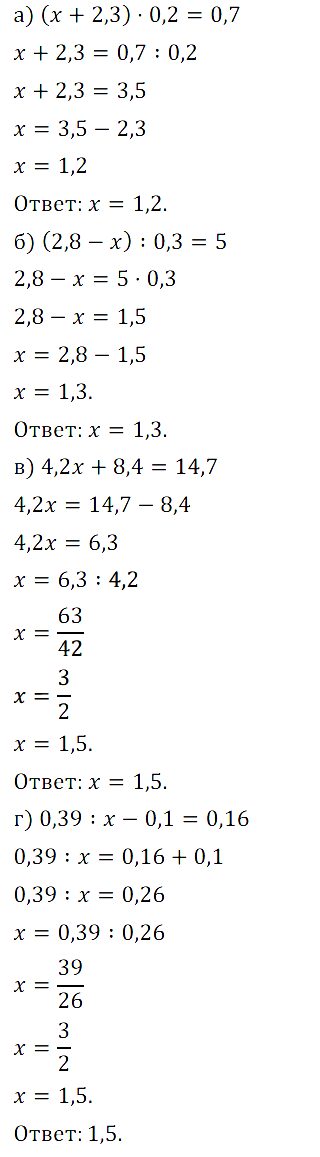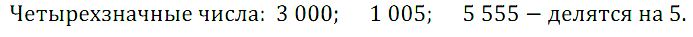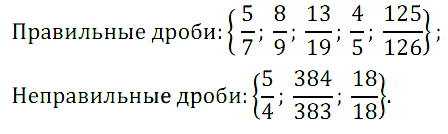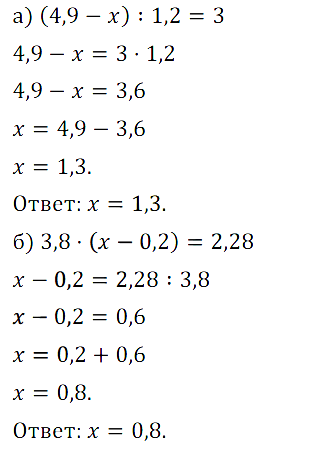Упражнения №№ 31-62 по математике из учебника УМК Виленкин с ответами. §1. Делимость чисел. 2. Признаки делимости на 10, на 5 и на 2. Математика 6 Виленкин. Задачи 31-62. Цитаты из учебника использованы в учебных целях. Ответы адресованы родителям.
Математика 6 класс Виленкин
2. Упражнения 31-62.
№ 31. Запишите натуральные числа от 1 до 30 в порядке возрастания и подчеркните красным карандашом каждое второе число, а синим — каждое пятое. Какие числа окажутся подчёркнуты красным карандашом, какие — синим?
Какие числа подчёркнуты обоими цветами?
Назовите числа, не делящиеся ни на 2, ни на 5.
№ 32. Назовите три числа, которые:
а) делятся на 2; в) делятся на 2 и на 5;
б) делятся на 5; г) не делятся ни на 2 и ни на 5.
№ 33. Назовите:
а) два чётных числа, кратных 5;
б) два нечётных числа, кратных 5;
в) два чётных числа, которые не делятся на 5;
г) два нечётных числа, которые не делятся на 5.
№ 34. Какие из чисел 200, 320, 3000, 50 000, 861, 76 540 делятся на 100? Какие из них делятся на 1000? Сформулируйте признаки делимости на 100, на 1000.
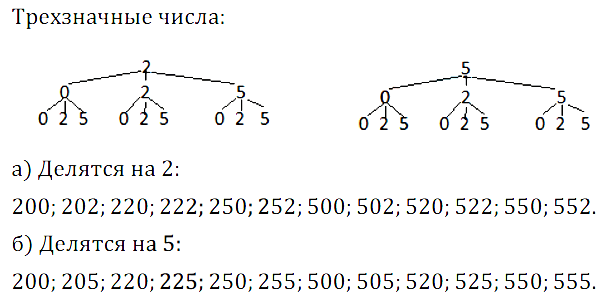
№ 35. Напишите множество трёхзначных чисел, в запись которых входят лишь цифры 0, 2, 5 и которые: а) делятся на 2; б) делятся на 5.
№ 36. Коля принёс несколько коробок с яйцами, по 10 яиц в каждой коробке. Может ли быть, что он принёс 35 яиц? 43 яйца? 50 яиц?
№ 37. Купили 5 одинаковых коробок цветных карандашей. Может ли в них оказаться: всего 92 карандаша? 90 карандашей? 75 карандашей?
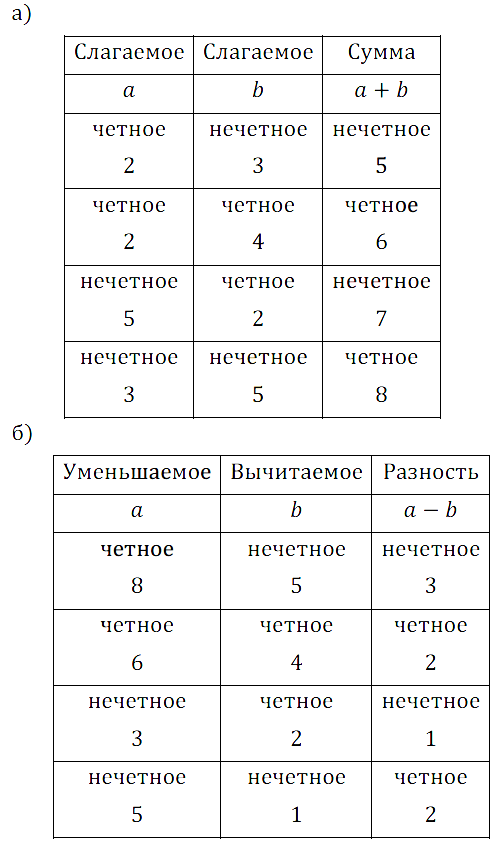
№ 38. Подставьте в таблицу подходящие значения а и b и сделайте вывод о чётности или нечётности результата действия.
№ 39. Можно ли, используя только цифры 3 и 4, записать:
а) число, которое делится на 10; в) число, кратное 5;
б) чётное число; г) нечётное число?
№ 40. Какие числа, кратные 5, удовлетворяют неравенству:
а) 64 < х < 78; б) 405 < х < 450; в) 24 < у < 49; г) 1 < у < 30?
№ 41. Вычислите устно:
а) 17 + 0,3; 0,05 + 25; 0,37 + 2,03; 3,84 + 0,2; 1,27 + 2,3;
б) 0,728 – 0,7; 0,8 – 0,25; 1 – 0,6; 0,7 – 0,07; 3 – 0,85;
в) 0,2 • 5; 4 • 2,5; 0,5 • 20; 0,24 • 1000; 2,7 • 100;
г) 2,6 : 2; 1,8 : 9; 3,7 : 10; 5,3 : 0,1; 6 : 0,3.
№ 42. Какие различные натуральные числа надо вписать в кружки (рис. 4), чтобы произведение каждых двух чисел, помещённых в кружках, соединённых отрезком, равнялось 70? Подумайте, как можно назвать набор чисел, оказавшихся в кружках.
№ 43. Если к числу прибавить 4, то полученное число разделится без остатка на 6. Чему равен остаток от деления первого числа на 6?
№ 44. На микрокалькуляторе по программе 12 |+| |=| получен результат 24. Попробуйте объяснить, почему получилось такое число. Подумайте, какие числа будут появляться на индикаторе после каждого нажатия клавиши |=| при выполнении программы:
8 |+| |=| |=| |=| |=| |=|.
№ 45. Подтвердите примерами следующее свойство суммы: а) если каждое слагаемое кратно числу а, то и сумма кратна числу а; б) если только одно слагаемое суммы не кратно числу а, то сумма не кратна числу а.
№ 46. Назовите наименьший и наибольший делители числа 24. Назовите наименьшее кратное числу 24. Есть ли у этого числа наибольшее кратное? Назовите какое–нибудь число, кратное и 5, и 12.
№ 47. Запишите все двузначные числа, являющиеся:
а) делителями 100; б) кратными 25; в) делителями 100 и кратными 25.
№ 48. Число b является делителем числа а. Докажите, что частное от деления а на b также является делителем числа а. Проверьте это утверждение, если а = 18, а b = 3.
№ 49. Докажите, что:
а) если а кратно b, а b кратно с, то а кратно с;
б) если а и b делятся на 6, то и а + b делится на 6.
№ 50. Какие из дробей 3/8, 8/5, 7/9, 5/4, 11/11, 2/3 являются правильными и какие — неправильными?
№ 51. При каких натуральных значениях а дробь (a – 3)/8 будет правильной и при каких натуральных значениях b дробь 9/(b + 2) будет неправильной?
№ 52. Решите уравнение:
а) (х + 2,3) • 0,2 = 0,7; в) 4,2х + 8,4 = 14,7;
б) (2,8 – х) : 0,3 = 5; г) 0,39 : х – 0,1 = 0,16.
№ 53. На уроке физкультуры Андрей, Марат, Костя, Саша, Петя и Серёжа готовятся к прыжкам в высоту.
а) Сколькими способами можно установить для них очерёдность прыжков?
б) Сколькими способами можно установить очерёдность прыжков, если начинают обязательно Костя или Саша?
№ 54. Решите задачу:
1) Я задумал число. Если его увеличить в 11 раз и результат уменьшить на 2,75, то получится 85,25. Какое число я задумал?
2) Я задумал число. Если его увеличить на 9,2 и результат увеличить в 11 раз, то получится 110. Какое число я задумал?
№ 55. Проверьте верность утверждения: «Многозначное число делится на 4, если число, образованное двумя его последними цифрами (цифрой десятков и цифрой единиц), делится на 4».
№ 56. Выпишите все числа в пределах трёхсот, которые кратны 25. Пронаблюдайте закономерность и сделайте вывод, какие числа делятся на 25.
№ 57. Дано множество А = {154, 161, 174, 178, 191, 315, 320, 346, 425, 475}. Составьте подмножество:
а) чисел, кратных 2; в) чисел, кратных 10;
б) чисел, кратных 5; г) нечётных чисел.
№ 58. Напишите:
а) все чётные числа, большие 10 и меньшие 21;
б) все нечётные числа, большие 12, но меньшие 23.
№ 59. Напишите три четырёхзначных числа, кратных 5.
№ 60. Дано множество дробей {5/7, 8/9, 13/19, 18/18, 5/4, 4/5, 125/126 и 384/383}. Составьте подмножество: а) правильных дробей; б) неправильных дробей.
№ 61. Решите уравнение: а) (4,9 – х) : 1,2 = 3; б) 3,8 • (х – 0,2) = 2,28.
№ 62. Найдите значение выражения:
а) (93 • 7 + 141) : 72;
б) (357 – 348 : 6) • 4;
в) 7091 + 9663 – (243 916 + 75 446) : 527 : 3;
г) 8607 + 7605 + (376 012 – 83 314) : 414 : 7.
Вы смотрели: Упражнения по математике для УМК Виленкин с ответами на некоторые задачи. §1. Делимость чисел. 2. Признаки делимости на 10, на 5 и на 2. Математика 6 Виленкин. Задачи 31-62. ГДЗ по новому учебнику (Решебник упражнений).