Математика Виленкин Учебник 4 «Виды треугольников» (задания №№ 1.134 — 1.163) из § 1 «ВЫЧИСЛЕНИЯ И ПОСТРОЕНИЯ». Ознакомительный фрагмент учебника 2023 года. Цитаты из учебного пособия использованы в учебных целях для семейного, заочного и дистанционного обучения.
Математика 6 класс (Виленкин, 2023) §1 п.4
<< §1 п.3 Вернуться в ОГЛАВЛЕНИЕ §1 п.5 >>
4. Виды треугольников
КЛЮЧЕВЫЕ СЛОВА • остроугольный, прямоугольный, тупоугольный треугольники • равносторонний, равнобедренный, разносторонний треугольники.
Из всех многоугольников наименьшее количество углов и сторон у треугольника. Среди окружающих нас предметов предметы в форме треугольника встречаются очень часто (рис. № 1.11).
В зависимости от вида углов различают следующие виды треугольников: остроугольные, прямоугольные и тупоугольные.
Треугольник называют:
• остроугольным, если все три его угла острые:
• прямоугольным, если один из его углов прямой;
• тупоугольным, если один из его углов тупой.
На рисунке 1.12 треугольник АКБ — остроугольный, треугольник CMD — прямоугольный, а треугольник PRH — тупоугольный с тупым углом R.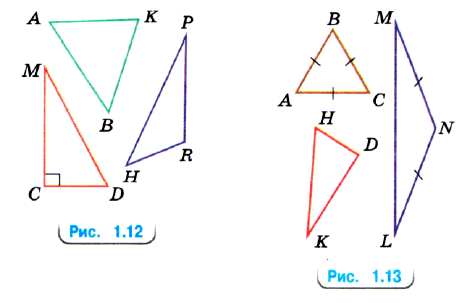
В зависимости от длин сторон различают следующие виды треугольников: равносторонние, равнобедренные и разносторонние.
Треугольник называют:
• равносторонним, если все три его стороны равны;
• равнобедренным, если только две его стороны равны;
• разносторонним, если все его стороны разной длины.
На рисунке 1.13 треугольник АВС — равносторонний, треугольник LMN — равнобедренный с боковыми сторонами LN и MN и основанием ML, а треугольник HDK — разносторонний.
Равные стороны и углы обозначают одинаковым числом штрихов и дуг соответственно.
Мы провели классификацию треугольников по углам и сторонам.
Пример 1. Используя линейку и транспортир, построим треугольник АВМ, у которого угол А равен 110°, сторона АВ равна 2 см, а сторона AM равна 3 см. (Говорят, построим треугольник по двум сторонам и углу между ними.)
Сначала, используя транспортир, построим угол А, равный 110° (рис. № 1.14, а).
Затем с помощью линейки на сторонах угла отложим от точки А отрезок АВ, равный 2 см, и отрезок AM, равный 3 см (рис. № 1.14, б).
Соединим точки В и М. Получили треугольник АВМ (рис. № 1.14, в).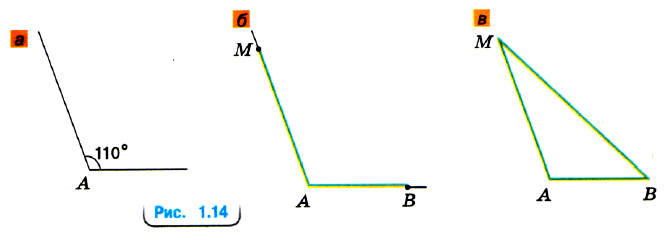
Пример 2. Используя линейку и транспортир, построим треугольник KHD, у которого угол К равен 30°, сторона КН равна 3 см, а угол Н равен 80°. (Говорят, построим треугольник по стороне и двум прилежащим к ней углам.)
Сначала, используя линейку, построим отрезок КН, равный 3 см (рис. № 1.15, а).
Затем с помощью транспортира отложим от луча КН угол, равный 30°, а от луча НК — угол, равный 80° как показано на рисунке 1.15, б.
Продлим стороны углов до пересечения в точке D. Получили треугольник KHD (рис. № 1.15, в).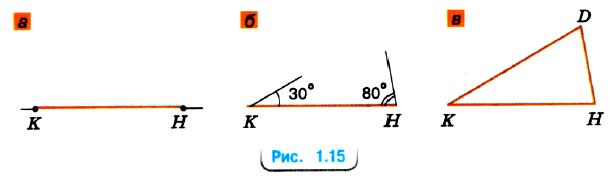
- Назовите виды треугольников при классификации их по углам.
- Назовите виды треугольников при классификации их по сторонам.
- Как построить треугольник по двум сторонам и углу между ними?
- Как построить треугольник по стороне и двум прилежащим к ней углам?
Упражнения № 1.134 – № 1.163
№ 1.134. На рисунке 1.16 изображены треугольники.
а) Используя чертёжный треугольник, определите и запишите виды треугольников по углам.
б) Используя линейку, определите и запишите виды треугольников по сторонам.
в) По результатам, полученным в пунктах а) и б), заполните таблицу на с. 34.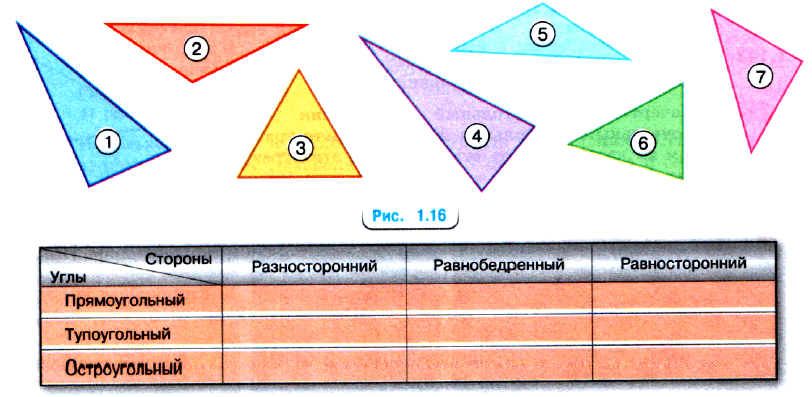
№ 1.135. Используя линейку и транспортир, постройте треугольник АВС, у которого;
а) угол А равен 60°, а стороны АВ и АС равны по 4 см;
б) угол А прямой, а стороны АВ и АС равны по 5 см;
в) угол А равен 120°, а стороны АВ и АС равны по 4 см.
Какой треугольник построен? Измерьте транспортиром его углы В и С.
Какое можно сделать предположение об углах при основании равнобедренного треугольника?
№ 1.136. а) Используя линейку и циркуль, постройте по алгоритму треугольник АВС, у которого сторона АВ равна 5 см, сторона АС = 3 см и сторона ВС = 4 см.
1. Начертите отрезок АВ, равный 5 см.
2. Проведите окружность с центром в точке А и радиусом 3 см.
3. Проведите окружность с центром в точке В и радиусом 4 см.
4. Обозначьте одну из точек пересечении окружностей буквой С.
5. Проведите отрезки АС и ВС.
б) Измерьте транспортиром угол С треугольника. Какой треугольник построен?
в) Используя линейку и циркуль, постройте по алгоритму равносторонний треугольник АВС, сторона которого равна 6 см.
№ 1.137. а) Постройте равнобедренный треугольник, у которого основание равно 4 см, а боковые стороны равны по 5 см.
б) Постройте равнобедренный треугольник, у которого основание равно 4 см, а боковые стороны равны по 6 см.
в) Можно ли построить равнобедренный треугольник, у которого основание равно 4 см, а боковые стороны равны по 2 см?
Сделайте предположение: «Сумма любых двух сторон треугольника… третьей стороны».
№ 1.138. Периметр одного треугольника в два раза больше другого. Могут ли эти треугольники быть равными?
№ 1.139. Всегда ли равны треугольники, у которых равны периметры?
№ 1.140. Одна сторона треугольника в два раза больше другой, а третьи сторона равна 15 см. Периметр треугольника равен 42 см. Найдите стороны треугольника.
№ 1.141. Могут ли стороны треугольника быть равными: а) 4 м, 4 м, 4 м; б) 3 см, 3 см, 12 см?
№ 1.142. Измерьте углы треугольника PRS на рисунке 1.17. Найдите сумму углов треугольника.
№ 1.143. а) Начертите прямоугольный треугольник АВС и остроугольный треугольник XZY. Измерьте транспортиром их углы. Найдите сумму углов в этих треугольниках.
б) Какое предположение можно сделать из решения задач № 1.142 и № 1.143, а?
- Свойство углов треугольника. Сумма углов треугольника равна 180°.
№ 1.144. Найдите угол треугольника, если два других угла равны 65° и 25°.
№ 1.145. Найдите углы треугольника, если два угла равны, а третий равен 130°.
№ 1.146. В треугольнике два угла равны, а третий угол равен 70°. Найдите углы треугольника. Рассмотрите два способа решения.
№ 1.147. Вычислите.
а) 0,01 + 1,1 + 0,09; 8,1 + 2,99 + 1,01; 1,88 + 3,7 + 0,12; 2,8 + 1,85 + 2,15; 1,07 + 0,88 + 1,93;
б) 15 – 2,3; 0,3 – 0,29; 7 – 0,2; 6 – 2,75; 16,4 – 4;
в) 2,5 • 2,7 • 4; 3,9 • 0,5 • 2; 1,25 • 1,9 • 8; 4 • 5,6 • 0,25; 0,5 • 30 • 0,1;
г) 1 : 10; 8,08 : 8; 9 : 100; 6,73 : 10; 0,3 : 0,1.
№ 1.148. Существуют ли натуральные значения с, при которых произведение 31с является простым числом?
№ 1.149. Может ли выражаться простым числом периметр или площадь прямоугольника, стороны которого выражены натуральными числами?
№ 1.150. Не выполняя вычислений, сравните значения выражений:
а) 14 • 0,76 и (14 • 76) : 100; в) 0,6 • 0,2 и (6 • 2): 100;
б) 340 • 0,02 и (340 • 2) : 10; г) 1,234 : 0,02 и 123,4 : 0,2.
№ 1.151. Фермер посадил на поле прямоугольной формы свёклу. Длина поля равна 73,4 м, что в полтора раза больше его ширины. Сколько свёклы фермер собрал с поля, если урожайность равна 2,25 ц с одного ара. Запишите полученный ответ в тоннах и килограммах.
№ 1.152. Масса ведра с водой равна 12,5 кг. После того как из ведра вылили половину воды, масса оставшейся воды с ведром стала 6,5 кг. Найдите массу пустого ведра.
№ 1.153. Решите уравнение: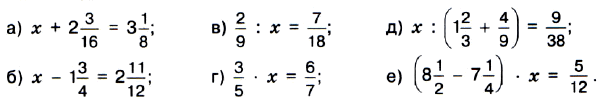
№ 1.154. Нарисуйте треугольник: а) прямоугольный; б) остроугольный; в) тупоугольный; г) равносторонний; д) равнобедренный; е) разносторонний; ж) тупоугольный и равнобедренный; з) остроугольный и равнобедренный; и) прямоугольный и равнобедренный.
№ 1.155. Используя линейку и транспортир, постройте треугольник MNK, у которого:
а) угол М равен 90°, сторона MN равна 7 см и МК равна 5 см;
б) угол М равен 60°, а стороны MN и МК равны по 6 см;
в) угол М равен 135°, а стороны MN и МК равны по 4 см.
Определите вид треугольников.
№ 1.156. Используя линейку и транспортир, постройте треугольник MNK, у которого:
а) угол М равен 90°, сторона MN равна 7 см и угол К равен 40°;
б) угол М равен 60°, сторона MN равна 7 см и угол К равен 60°;
в) угол М равен 30°, сторона MN равна 7 см и угол К равен 30°.
Определите вид треугольников.
№ 1.157. Найдите периметр треугольника со сторонами 6,1 см, 5,7 см, 10,2 см.
№ 1.158. Найдите периметр треугольника АВС, если сторона АВ равна 18 см, сторона АС в два раза больше стороны АВ, а сторона ВС на 10 см меньше стороны АС.
№ 1.159. Найдите сторону равностороннего треугольника, если его периметр равен 6,09 дм.
№ 1.160. В треугольнике KLM угол KLM равен 80°, а угол MKL в 4 раза меньше. Найдите угол KML.
№ 1.161. В треугольнике АВС угол А в 2 раза больше угла В и на 20° меньше угла С. Найдите углы треугольника АВС.
№ 1.162. Найдите корень уравнения:
а) (2 – 1 2/3) • х = 5/9; б) х : (2/3 + 1/9) = 9/35.
№ 1.163. Вычислите:
а) 51 – (3,75 : 3 + 86,45 : 24,7) • 2,4; б) (650 000 : 3125 – 196,5) • 3,14.

Вы смотрели: Математика Виленкин Учебник 4 «Виды треугольников» (задания №№ 1.134 — 1.163) из § 1 «ВЫЧИСЛЕНИЯ И ПОСТРОЕНИЯ». Ознакомительный фрагмент учебника 2023 года.
<< §1 п.3 Вернуться в ОГЛАВЛЕНИЕ §1 п.5 >>