Математика 6 класс для УМК Мерзляк и др. § 2 «Признаки делимости на 10, на 5 и на 2» (2014-2017 годы). Ответы и решения некоторых задач из старого учебника. Математика 6 Мерзляк. Упр. 40-72.
ОГЛАВЛЕНИЕ (2014 год) ОГЛАВЛЕНИЕ (2021 год)
Обратите внимание! Вы смотрите старую редакцию учебника!
§2. Признаки делимости на 10, на 5 и на 2.
Решаем устно
№ 1. Верно ли утверждение: 1) число 17 является делителем числа 34;
2) число 5 является делителем числа 35; 3) число 45 является кратным числа 10; 4) число 17 кратно числу 2?
Правильный ответ: 1) да; 2) да; 3) нет; 4) нет.
№ 2. Назовите четыре натуральных числа, для которых делителем является число: 1) 2; 2) 7.
Правильный ответ: 1) 4, 6, 8, 10; 2) 14, 21,28.35.
№ 3. Назовите четыре натуральных числа, кратных числу: 1) 5; 2) 11.
Правильный ответ: 1) 10,15,20,25; 2) 22,33,44,55.
№ 4. Назовите в порядке возрастания все делители числа: 1) 6; 2) 14; 3) 40; 4) 9; 5) 7.
Правильный ответ: 1) 1, 2, 3, 6; 2) 1, 2, 7, 14; 3) 1, 2, 4, 5, 8, 10, 20, 40; 4) 1,3.9; 5) 1,7.
Упражнения 40 — 72
№ 40. Заполните таблицу (поставьте знак «+» в случае утвердительного ответа или знак «-» в ином случае).
| Число | 24 | 53 | 60 | 78 | 79 | 96 | 142 | 241 | 495 | 7207 |
| Чётное число |
Правильный ответ:
| Число | 24 | 53 | 60 | 78 | 79 | 96 | 142 | 241 | 495 | 7207 |
| Чётное число | + | — | + | + | — | + | + | — | — | — |
№ 41. Из чисел 34, 467, 435, 860, 648, 5 465, 8 216, 2 405, 1 020, 246 370 выпишите те, которые делятся нацело: 1) на 2; 2) на 5; 3) на 10.
Правильный ответ: 1) делятся нацело на 2: 34, 860, 648, 8216, 1020, 246370;
2) делятся нацело на 5: 435, 860, 5465, 2405, 1020, 246370;
3) делятся нацело на 10: 860, 1020, 246370.
№ 42. Какие из чисел 68, 395, 760, 943, 1 270, 2 625, 9 042, 7 121, 1 734: 1) не делятся нацело на 2; 2) кратны 10; 3) делятся нацело на 5, но не делятся нацело на 10?
Правильный ответ: 1) не делятся нацело на 2: 395, 943, 2625, 7121;
2) кратны 10: 760, 1270;
3) делятся нацело на 5, но не делятся нацело на 10: 395, 2625.
№ 43. Верно ли утверждение: 1) сумма двух чётных чисел является чётным числом; 2) сумма двух нечётных чисел является нечётным числом; 3) сумма чётного и нечётного чисел является нечётным числом; 4) если сумма двух чисел является чётным числом, то и слагаемые — чётные числа; 5) произведение двух чётных чисел является чётным числом; 6) произведение двух нечётных чисел является нечётным числом; 7) произведение чётного и нечётного чисел является нечётным числом?
Правильный ответ: 1) сумма двух чётных чисел является чётным числом — верно;
2) сумма двух нечётных чисел является нечётным числом — НЕверно;
3) сумма чётного и нечётного чисел является нечётным числом — верно;
4) если сумма двух чисел является чётным числом, то и слагаемые — чётные числа — НЕверно;
5) произведение двух чётных чисел является чётным числом — верно;
6) произведение двух нечётных чисел является нечётным числом — НЕверно;
7) произведение чётного и нечётного чисел является нечётным числом — НЕверно.
№ 44. Запишите все нечётные значения х, при которых верно неравенство: 1) 273 < х < 290; 2) 2 725 < х < 2 737.
Правильный ответ: 1) 273 < х < 290: 273, 275, 277, 279, 281, 283, 285, 287, 289;
2) 2 725 < х < 2 737: 2727, 2729, 2731, 2733, 2735.
№ 45. Запишите все чётные значения х, при которых верно неравенство: 1) 134 < х < 160; 2) 489 < х < 502.
Правильный ответ: 1) 134 < х < 160: 136, 138, 140, 142, 144, 146, 148, 150, 152, 154, 156, 158;
2) 489 < х < 502: 490, 492, 494, 496, 498, 500.
№ 46. Найдите все значения х, кратные числу 5, при которых верно неравенство: 1) 38 < х < 75; 2) 3 720 < х < 3 754.
Правильный ответ: 1) 40, 45, 50, 55, 60, 65, 70;
2) 3725, 3730, 3735, 3740, 3745, 3750.
№ 47. Найдите все значения х, кратные числу 10, при которых верно неравенство: 1) 279 < х < 320; 2) 1 465 < х < 1 510.
Правильный ответ: 1) 280, 290, 300, 310; 2) 1470, 1480, 1490, 1500.
№ 48. Запишите все четырёхзначные числа, кратные числу 5, для записи которых используют цифры 0, 3, 5, 7 (цифры не могут повторяться).
Правильный ответ: 3570, 3750, 5350, 5730, 7035, 7350, 7530.
№ 49. Найдите все цифры, которые можно дописать справа к числу 793, чтобы получить число, кратное: 1) 2; 2) 5; 3) 10 (можно дописывать только одну цифру).
Правильный ответ: 1) 0, 2, 4, 6, 8; 2) 0, 5; 3) 0.
№ 50. Запишите наибольшее: 1) четырёхзначное число, кратное 2; 2) пятизначное число, кратное 5; 3) шестизначное число, кратное 10. Цифры в записи числа не могут повторяться.
Правильный ответ: 1) 9876; 2) 98765; 3) 987650.
№ 51. 1) Запишите шесть первых натуральных чисел, кратных 100. Обратите внимание на две последние цифры этих чисел. Сформулируйте признак делимости на 100.
2) Запишите восемь первых натуральных чисел, кратных 25. Обратите внимание на две последние цифры этих чисел. Сформулируйте признак делимости на 25.
Правильный ответ: 1) 100, 200, 300, 400, 500, 600. Если число оканчивается двумя нулями, то оно делится на 100.
2) 25, 50, 75, 100, 125, 150, 175, 200. Число делится на 25, если две его последние цифры — нули или образуют число, которое делится на 25.
№ 52. Найдите наибольшее двузначное число х, при котором значение выражения х — 32 делится нацело на 5.
Правильный ответ: Число х — 32 делится нацело на 5, значит оно должно оканчиваться 5 или 0. Следовательно, если число х двузначное и наибольшее, то х = 97.
№ 53. Найдите наименьшее трёхзначное число г/, при котором значение выражения 327 + у является числом, кратным 10.
Правильный ответ: Число 327 + у делится нацело на 10, значит оно оканчивается на ноль. Следовательно, если число у трехзначное и наименьшее, то у = 103.
№ 54. Может ли число, в записи которого все цифры равны 1, делиться нацело на число, в записи которого все цифры равны 2?
Правильный ответ: Нет, так как число состоящее из одних единиц, делится нацело только на само себя и 1, а число, состоящее из одних двоек, делится нацело на число, состоящее из одних единиц, 2 и 1.
№ 55. Может ли число, в записи которого все цифры равны 2, делиться нацело на число, в записи которого все цифры равны: 1) 1; 2) 5?
Правильный ответ: 1) Да, так как любое число делится на 1.
2) Нет, по признаку делимости на 5.
№ 56. 1) Сумма двух натуральных чисел является нечётным числом. Чётным или нечётным числом будет их произведение?
2) Сумма двух натуральных чисел является чётным числом. Обязательно ли их произведение будет чётным числом?
Правильный ответ: 1) Пусть а — четное число, а другое число b + 1 — нечетное число, где b — четное. Значит их произведение будет а * b + а. Так как здесь все числа четные, то и а * b + а — четное.
2) Нет, необязательно. Если натуральные числа четные, то и их произведение будет четным 2 • 4 = 8, а если числа нечетные, то и произведение будет нечетным 3 • 5 = 15.
№ 57. Чётной или нечётной будет сумма семи натуральных слагаемых, если: 1) четыре слагаемых чётные, а остальные — нечётные; 2) четыре слагаемых нечётные, а остальные — чётные?
Правильный ответ: 1) нечетной; 2) четной.
№ 58. Сумма девяти натуральных слагаемых равна 1 000. Можно ли утверждать, что их произведение — чётное число? Ответ объясните.
Правильный ответ: Так как чисел 9, то среди них есть обязательно четное, а значит и их произведение четное число.
№ 59. Можно ли разложить 50 яблок на пять кучек, в каждой из которых нечётное количество яблок? Ответ объясните.
Правильный ответ: Нет, нельзя, так как сумма 5 нечетных чисел — нечетное число, а число 50 — четное.
№ 60. Существует ли прямоугольник, длины сторон которого выражены натуральными числами в сантиметрах, причём одна из них на 1 см длиннее другой, и площадь которого равна 12 345 см2?
Правильный ответ: Нет, так как по условиям задачи разница между сторонами 1 см, то одна из сторон четная, а другая нечетная. А значит их произведение — четное число. А не 12345 см2.
№ 61. Известно, что га — натуральное число. Является ли чётным числом значение выражения: 1) 2га; 3) га(га + 1); 5) (2га + 5)(4га — 2)(2га + 7)? 2) 2га + 1; 4) (2га — 1)(2га + 3);
Правильный ответ: 1) да; 2) нет; 3) да; 4) нет; 5) да.
№ 62. В школе работают два ночных охранника — Иван Иванович и Пётр Петрович. Они дежурят по очереди с вечера до утра следующего дня. Иван Иванович заступил на дежурство 1 сентября, а Пётр Петрович — 2 сентября. Кто из них заступит на дежурство 18 сентября? 29 сентября? 1 октября? 30 октября? 31 октября? По каким числам — чётным или нечётным — будет дежурить Иван Иванович в ноябре? Кто из них будет дежурить в ночь на Новый год?
Правильный ответ: 18 сентября — Пётр Петрович; 19 сентября — Иван Иванович; 1 октября — Иван Иванович; 30 октября — Пётр Петрович; 31 октября — Иван Иванович. В ноябре Иван Иванович будет дежурить по четным числам. На новый год будет дежурить Пётр Петрович.
№ 63. Верно ли, что из любых трёх натуральных чисел всегда найдутся два таких, сумма которых делится нацело на 2?
Правильный ответ: Верно, так как или эти два числа будут четными, или они оба будут нечетными.
№ 64. Сколькими нулями оканчивается запись числа, которое равно произведению: 1) 1 • 2 • 3 … 15 • 16; 2) 1 • 2 • 3 … 25 • 26?
Правильный ответ: 1) тремя; 2) пятью.
№ 65. Сумма двух натуральных чисел равна 700. Первое из них оканчивается цифрой 7. Если её зачеркнуть, то получим второе число. Найдите эти числа.
Правильный ответ: 637 + 63 = 700.
№ 66. Сколько существует двузначных чисел, для записи которых использованы только: 1) чётные цифры; 2) нечётные цифры?
Правильный ответ: 1) 20 чисел; 2) 25 чисел.
№ 67. Можно ли в выражении 1 + 2 + 3 + 8 + 9 заменить некоторые знаки «+» на знаки «-» так, чтобы значение полученного числового выражения было равным 18?
Правильный ответ: Нет, нельзя. Так как сумма данных чисел — нечетное число, то при замене знаков выражение останется нечетным числом, а 18 — четное число.
№ 68. Докажите, что: 1) 14 168 кратно 28; 3) 73 является делителем 14 892; 2) 1 878 не кратно 24; 4) 56 не является делителем 5 172.
№ 69. По состоянию на 2008 год в России было 57 естественнонаучных и научно-технических музеев. Сколько всего музеев каждого из этих видов, если научно-технических музеев в 2 раза меньше, чем естественнонаучных?
Правильный ответ: 1) 57 : (2 +1) = 19 — научно-технических музеев.
2) 19 • 2 = 38 — естественнонаучных музеев.
№ 70. По состоянию на 2008 год в России был 141 государственный природный заповедник и национальный парк. Сколько в России природных заповедников и сколько национальных парков, если заповедников на 61 больше, чем парков?
Правильный ответ: 1) (141 — 61) : 2 = 40 парков.
2) 40 + 61 = 101 заповедник.
№ 71. Выполните действия: 1) (69 • 0,63 — 10,098 : 5,4 — 20,54) : 0,324; 2) 0,98 • 3,8 — 0,132 : 5,5 — 2,45.
№ 72. В клетках таблицы размером 3X3 стоят нули. Разрешается выбрать любой квадрат размером 2X2 клетки и увеличить числа во всех его клетках на единицу. Можно ли после нескольких таких операций получить таблицу, изображённую на рисунке 1?
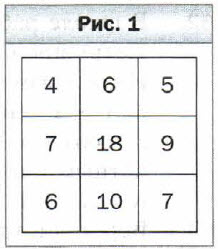
Правильный ответ: В центре таблицы стоит число 18, значит всего было проведено 18 операций. Но так как сумма чисел по углам квадрата равна 4 + 5 + 7 + 6 = 22, то было проведено 22 операции, следовательно, получить данную таблицу нельзя.
ОГЛАВЛЕНИЕ (2014 год) ОГЛАВЛЕНИЕ (2021 год)
Вы смотрели: Математика 6 класс для УМК Мерзляк и др. § 2 «Признаки делимости на 10, на 5 и на 2» (2014 год). Ответы и решения некоторых задач. Математика 6 Мерзляк. Упр. 40-72. ГДЗ для учебника. Решебник некоторых упражнений из старого учебника «Математика 6 класс».

