Математика Дорофеев Учебник §1.1 «Что мы знаем о дробях» онлайн версия для ознакомления и покупки учебника «Математика. 6 класс / Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. — М.: Просвещение». Цитаты из учебника 2016 года использованы в учебных целях для семейного, заочного и дистанционного обучения.
Математика 6 класс (Дорофеев) § 1.1.
<< § 12.3 Вернуться в ОГЛАВЛЕНИЕ § 1.2 >>
Глава 1. Дроби и проценты
Каждый день вы произносите слова «минута» и «секунда». А знаете ли вы, что значение этих слов связано с дробями? Пришедшее к нам из латинского языка слово «минута» близко по значению словам «маленький», «уменьшать». Это связано с его происхождением — минута появилась тогда, когда стала необходимой единица измерения углов, меньшая градуса. А название «секунда» понятно каждому, кто изучает английский или французский языки. Оно тоже латинского происхождения и означает «второй». Минута – это первый шаг уменьшения (градус разделили на 60 равных частей), а секунда – второй (минуту разделили на 60 равных частей).
§ 1.1. Что мы знаем о дробях
С самых древних времён, наряду с необходимостью считать предметы, у людей появилась потребность в измерении длин, площадей, углов и других величин. Используемые единицы измерения часто не укладывались в измеряемой величине целое число раз. Для получения более точных результатов меры стали делить на части, что привело к появлению дробей.
В Древнем Вавилоне за 2000 лет до н. э. при измерениях величин применяли шестидесятые доли. Вавилоняне изобрели систему измерения углов, которая используется и поныне. Учёные в Древнем Вавилоне понимали, что при измерении углов в астрономии, архитектуре, мореплавании нельзя ограничиваться лишь целым числом градусов, так как при этом расчёты оказываются очень неточными. Поэтому они стали использовать более мелкие единицы. Градус разделили на 60 равных частей — минут: в градусе 60 минут, так что 1 минута — это 1/60 часть градуса. Для большей точности минуту разделили ещё на 60 частей и получили секунды: в минуте 60 секунд, так что 1 секунда — это — часть минуты.
Вообще, первыми в практике людей появились самые простые дроби, составляющие одну долю целого (1/2, 1/3, 1/4 и т.д.). И вначале люди для вычислений употребляли только такие дроби. Лишь значительно позже греки, а затем индусы стали использовать в вычислениях и другие дроби.
Запись дробей с помощью числителя и знаменателя появилась в Древней Греции, только греки знаменатель записывали сверху, а числитель — снизу. В привычном для нас виде дроби впервые стали записываться в Древней Индии около 1500 лет назад, но при этом индусы обходились без черты между числителем и знаменателем. Общеупотребительной черта дроби стала только с XVI в.
В современной записи, как вам известно, дроби выглядят так: 2/3, 3/100, 17/10. Знаменатель (число, записанное под чертой) показывает, на сколько равных долей делили целое; числитель (число, записанное над чертой) показывает, сколько таких долей взято.
Интересно, что в языках разных народов слова для обозначения понятия «дробь» происходят от таких глаголов, как «раздроблять», «разбивать», «ломать». А в первых русских учебниках математики дроби так и назывались— «ломаные числа».
□ Назовите числитель и знаменатель каждой дроби и расскажите, что они показывают: 1/2, 3/7, 8/5.
□ Какую долю развёрнутого угла составляет 1°? Какую долю 1 часа составляет 1 минута? Какую долю 1 м составляет 1 см? Запишите ответ с помощью дроби.
□ Какая часть фигуры закрашена (рис. 1.1, а–д)?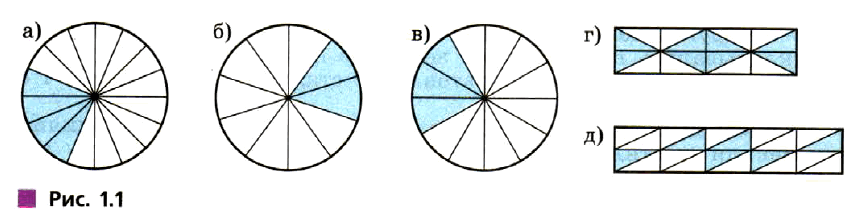
Для каждой дроби существует бесконечно много дробей, равных ей. Например: 1/3 = 2/6 = 4/12 = … . Преобразовывать дробь в равную позволяет основное свойство дроби:
Применяя это свойство, можно приводить дроби к новому знаменателю, сокращать дроби.
Примеры 1-3
Пример 1. Приведём дробь — к знаменателю 36. Сначала найдём дополнительный множитель: 36 : 3 = 12. Теперь умножим числитель и знаменатель дроби на 12: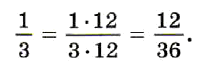
Заметим, что дробь 1/3 можно привести к любому знаменателю, кратному 3, т. е. к 6, 9, 12 и любому другому числу, делящемуся на 3. Однако эту дробь нельзя привести, например, к знаменателю 10, так как число 10 на 3 не делится.
Пример 2. Сократим дробь 162/270. Будем выполнять сокращение последовательно:![]()
Сначала мы разделили числитель и знаменатель на 2. Потом воспользовались признаком делимости на 9 и сократили полученную дробь на 9. И наконец, разделили числитель и знаменатель на 3. Понятно, что можно было выполнить цепочку сокращений иначе, например сразу заметить, что числитель и знаменатель делятся на 9.
Пример 3. Сравним дроби 7/12 и 5/9. Приведём дроби к общему знаменателю. Вы знаете, что в качестве общего знаменателя дробей можно взять произведение знаменателей 12 и 9, т. е. число 108. Но если мы хотим найти наименьший общий знаменатель, то будем действовать с помощью известного вам приёма: будем последовательно перебирать числа, кратные 12 — большему знаменателю, и проверять, делятся ли они на 9. Число 24 на 9 не делится, а 36 уже делится. Дополнительный множитель для первой дроби равен 36 : 12 = 3, для второй дроби он равен 36 : 9 = 4. Получаем: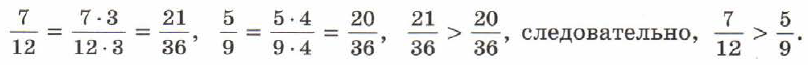
□ Сформулируйте основное свойство дроби и проиллюстрируйте его примером.
□ Запишите закрашенную часть фигуры разными способами (см. рис. 1.1).
□ Объясните на примере дробей 8/15 и 7/9, как привести дроби к наименьшему общему знаменателю.
Задания 1–7 группы А
№ 1. Моделируем. Изобразите какую-нибудь геометрическую фигуру (прямоугольник, круг или отрезок) и закрасьте её часть, которая соответствует дроби:
а) 5/8; б) 7/9; в) 8/12; г) 15/25.
№ 2. Действуем по алгоритму. 1) Приведите дроби:
а) 4/9, 5/6, 7/2 к знаменателю 18; б) 7/8, 5/16, 21/40 к знаменателю 80.
2) Приведите к наименьшему общему знаменателю дроби:
а) 1/3 и 1/4; б) 5/8 и 3/16; в) 5/8 и 3/20; г) 2/9 и 7/24.
№ 3. В Древнем Риме при измерении величин применялись дроби со знаменателем 12. Вместо 1/12 говорили «одна унция», вместо 5/12 – «пять унций» и т. п. Выразите в унциях: половину, треть, четверть, пять шестых, три четверти.
№ 4. Сократите дробь:
а) 24/30; б) 12/48; в) 20/36; г) 14/56; д) 44/100; е) 36/60.
№ 5. Ищем способ сравнения. Сравните дроби и запишите результат сравнения с помощью знаков >, <, =. В каждом случае расскажите, каким способом вы действовали: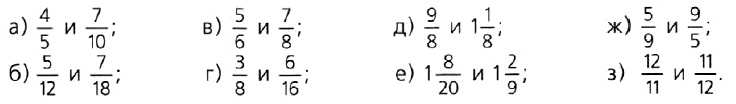
№ 6. Запишите дроби в порядке возрастания:
№ 7. а) На тренировке Оля пробежала стометровку за 1/3 мин, Галя — за 17/60 мин, Вера – за 3/10 мин, Зоя – за 4/15 мин. В каком порядке девочки пришли к финишу, если они стартовали одновременно?
б) На путь от школы до стадиона Толя и три его друга затрачивают разное время: Толя – 2/5 ч, Саша – 1/2 ч, Коля 3/10 ч, Петя – 7/12 ч. Ребята вышли из школы одновременно. В каком порядке они придут на стадион?
Задания 8–16 группы Б
№ 8. Покажите, что верны равенства:
a) 5/9 = 55/99 = 555/999; б) 13/77 = 1313/7777 = 131313/777777.
№ 9. Сократите дробь (9–10).
9. а) 78/338; б) 700/840; в) 255/525; г) 324/405.
№ 10. а) (84 • 108) / (48 • 126); б) (96 • 35 • 110) / (33 • 80 • 105).
№ 11. Ищем способ решения. Найдите какие-нибудь три числа, которые:
а) больше 1/7, но меньше 2/7; б) меньше 5/9, но больше 4/9.
№ 12. Рассуждаем. Не приводя дроби к общему знаменателю, установите, какая из них наибольшая:
а) 11/20, 21/40, 31/60; б) 23/48; 17/36; 35/72.
№ 13. Исследуем. 1) Дана правильная дробь 2/3. Запишите обратную ей дробь. Правильной или неправильной является эта дробь? Какая из этих двух дробей ближе к 1?
2) Запишите какую-нибудь правильную дробь и дробь, обратную ей. Какая из них ближе к 1? Проведите такой эксперимент ещё раз.
3) Какая из дробей ближе к 1 – правильная или обратная ей неправильная? Поясните свой вывод.
№ 14. Запишите координаты каждой точки, отмеченной на координатной прямой (рис. 1.2).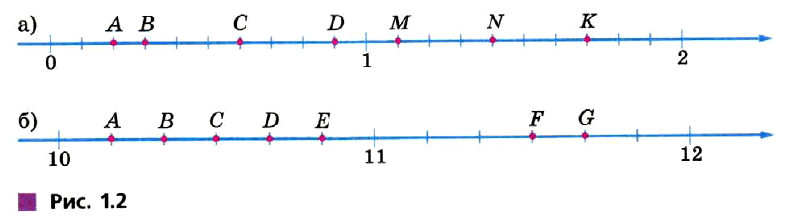
№ 15. Начертите координатную прямую (возьмите единичный отрезок, равный 12 клеткам). Отметьте на ней числа: 1/6, 5/6, 1/3, 2/3, 1 2/3, 1/12, 5/12, 1 7/12, 1/2, 1 1/2.
№ 16. Какой из отрезков (рис. 1.3) имеет наибольшую длину? Как он называется? Воспроизведите рисунок (радиус задайте самостоятельно).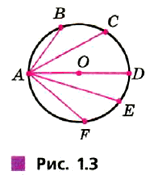
Вы смотрели: Математика Дорофеев Учебник §1.1 онлайн версия для ознакомления и покупки учебника «Математика. 6 класс / Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. — М.: Просвещение».
<< § 12.3 Вернуться в ОГЛАВЛЕНИЕ § 1.2 >>