Математика Виленкин Учебник 1 «Среднее арифметическое» (задания 1.1 — 1.40) из § 1 «ВЫЧИСЛЕНИЯ И ПОСТРОЕНИЯ». Ознакомительный фрагмент учебника 2023 года. Цитаты из учебного пособия использованы в учебных целях для семейного, заочного и дистанционного обучения.
Математика 6 класс (Виленкин, 2023) §1 п.1
<< §6 п.44 Вернуться в ОГЛАВЛЕНИЕ §1 п.2 >>
Глава I Смешанные числа
§ 1. Вычисления и построения
§ 2. Действия со смешанными числами
§ 3. Отношения и пропорции
§ 1. Вычисления и построения.
1. Среднее арифметическое
КЛЮЧЕВЫЕ СЛОВА: • среднее арифметическое • средняя скорость.
Задача 1. Три девочки собирали клубнику. Первая собрала 8 кг, вторая 9 кг, а третья 4 кг. Всю клубнику они поделили поровну. Сколько килограммов клубники получила каждая девочка?
Решение. Девочки собрали 8 + 9 + 4, т. е. 21 кг клубники. Каждой досталось 21 : 3, т. е. по 7 кг клубники.
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
Среднее арифметическое = (сумма чисел) : (количество слагаемых)
Задача 2. Катамаран плыл 4 ч со скоростью 16,1 км/ч и 3 ч со скоростью 15,4 км/ч. Найдите постоянную скорость, с которой он должен был плыть, чтобы проплыть это расстояние за то же время.
Решение. Расстояние, которое проплыл катамаран, равно
16,1 • 4 + 15,4 • 3 = 64,4 + 46,2 = 110,6 (км).
Разделим расстояние на время, затраченное на этот путь:
110,6 : (3 + 4) = 110,6 : 7 = 15,8 (км/ч).
Ответ. Катамаран должен был плыть с постоянной скоростью 15,8 км/ч.
Такую скорость называют средней скоростью движения, и она равна частному от деления пройденного пути на время движения.
Ответ задачи можно получить, если найти среднее арифметическое скоростей:
(16,1 + 16,1 + 16,1 + 16,1 + 15,4+ 15,4+ 15,4) : 7= 15,8 (км/ч).
Подобным образом находят среднюю урожайность, среднюю производительность и т. д.
В повседневной жизни часто используются средние арифметические значения величин. Например, средняя рождаемость в городе, среднее потребление сахара за год жителями страны, средний балл по математике за третью четверть в классе и многое другое.
Среднее арифметическое позволяет сравнивать числовые показатели величин одного типа. Например, если среднее арифметическое температур в августе равно 19,1 °С, а в июле 18,9 °С, то июль оказался холоднее августа.
- Что называют средним арифметическим нескольких чисел?
- Как найти среднее арифметическое нескольких чисел?
- Как найти среднюю скорость движения?
- Приведите примеры средних арифметических величин.
Упражнения № 1.1 – № 1.40
№ 1.1. Отметьте на координатной прямой числа 4 и 12. Найдите их среднее арифметическое и тоже отметьте его на координатной прямой. Какое предположение можно сделать?
№ 1.2. На рисунке 1.1 отрезки NM и NK равны. Найдите координату точки М. Найдите среднее арифметическое координат точек М и К.
№ 1.3. Найдите среднее арифметическое чисел:
а) 83,4 и 84,5; в) 2,23; 2,26; 2,34 и 2,07;
б) 0,2; 0,3 и 0,4; г) 6,276; 5,864; 7,223; 9,106; 8,728 и 3,003.
№ 1.4. В течение недели ноября ежедневно в 12 часов дня школьники записывали следующие показания термометра: 4,1; 3,8; 4,1; 4,2; 4,1; 4,0; 3,9 градусов тепла. Найдите среднюю температуру за эту неделю в 12 ч дня.
№ 1.5. У ученика за четверть по литературе стоят следующие оценки: 5, 3, 4, 4, 5, 5, 4, 3, 5, 4. Найдите среднюю оценку ученика за четверть.
№ 1.6. Чему равно среднее арифметическое чисел 42,43; 42,39; 42,64 и 42,57? Округлите его до сотых.
№ 1.7. Пешеход шёл 2 ч со скоростью 5,2 км/ч, 2 ч со скоростью 4,8 км/ч и 1 ч со скоростью 4,5 км/ч. Чему равна средняя скорость пешехода на всём пути?
№ 1.8. Экскурсионный теплоход двигался 4,3 ч по озеру со скоростью 106,4 м/мин, затем 2,5 ч по реке со скоростью 24 км/ч, наконец, 1,2 ч по заливу со скоростью 10 км/ч. Найдите среднюю скорость движения теплохода на всём пути.
№ 1.9. Черепаха бежала 5 мин со скоростью 70,2 м/мин и 2 мин со скоростью 106,4 м/мин. Найдите среднюю скорость черепахи на пройденном за это время пути.
№ 1.10. На первом поле вырастили 5264 ц помидоров, а на втором – 5425 ц. Найдите урожайность помидоров на каждом из этих полей и найдите среднюю урожайность на двух этих полях, если площадь первого поля равна 29 га, а второго – 33 га. Округлите результат до сотен. Предложите другой способ решения этой задачи.
№ 1.11. Первое число равно 7. Чему равно второе число, если среднее арифметическое двух чисел равно 5,3?
№ 1.12. Среднее арифметическое четырнадцати чисел равно 4,5, а среднее арифметическое шести других чисел — 2,75. Найдите среднее арифметическое этих двадцати чисел.
Сумма чисел равна среднему арифметическому, умноженному на количество чисел.
№ 1.13. На первом участке трассы лыжник шёл 3 ч с некоторой скоростью, а на втором — 2 ч со скоростью 25 км/ч. Найдите скорость лыжника на первом участке трассы, если его средняя скорость на трассе равна 28 км/ч.
№ 1.14. Скорость теплохода по течению 20,8 км/ч, а против течения 14,4 км/ч. Найдите собственную скорость теплохода и скорость течения.
№ 1.15. Среднее арифметическое двух чисел равно 42. Чему равны эти числа, если одно из них в 2,5 раза меньше другого?
№ 1.16. Вычислите.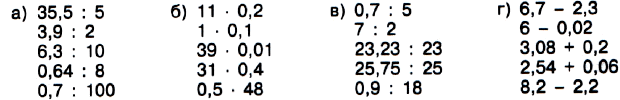
№ 1.17. Найдите частное:
а) 60 : 0,6; б) 0,9 : 0,3; в) 40 : 0,2; г) 100 : 0,1; д) 1000 : 0,01; е) 8 : 0,4; ж) 0,42 : 0,7; з) 0,1 : 0,01; и) 1 : 0,5.
№ 1.18. При покупке красных гвоздик в упаковках оказалось 35, 26, 39, 28, 20, 26, 29 цветов. Можно ли из всех этих цветов сделать 7 одинаковых букетов?
Вы знаете, что: 0,1 = 1/10; 0,25 = 1/4; 0,2 = 1/5; 0,125 = 1/8; 0,5 = 1/2. Поэтому умножить число на 0,25 означает найти четверть числа; умножить на 0,2 означает найти пятую часть числа и т. д.
№ 1.19. Как проще всего найти произведение: а) 7000 • 0,1; б) 600 • 0,2; в) 48 • 0,25; г) 32 • 0,125; д) 114 • 0,5?
№ 1.20. 1) Может ли произведение двух чисел оказаться меньше: а) одного из множителей; б) обоих множителей? Приведите примеры.
2) Может ли частное оказаться больше делимого? Приведите примеры.
№ 1.21. Папе, чтобы купить нужное количество материалов для починки забора, нужно определить его длину, но нет рулетки. Петя заметил, что расстояние между двумя соседними столбиками забора равно пяти его шагам, а столбиков всего 40. Чему равна длина забора, если один шаг мальчика 0,45 м? Сколько решений имеет задача?
№ 1.22. Найдите частное:
а) 0,468 : 0,26; в) 3,648 : 4,56; д) 50,02 : 41;
б) 0,9775 : 0,425; г) 0,559 : 0,043; е) 142,4 : 178.
№ 1.23. Найдите корень уравнения:
а) 4,1x – 2,9x + 7,5 = 7,98; б) 7,8у – (5,6у + 10,6) = 3,7;
в) (8,3 – z) • 4,9 = 5,88; г) (11,2 – р) • 4,5 = 31,5.
№ 1.24. Центр аттракционов занимает 14400 м2, что составляет 0,01 всего парка. Найдите площадь парка и выразите её в квадратных километрах.
№ 1.25. В 10 ч легковой автомобиль догнал грузовой, а в 19 ч был впереди него на 180 км. Какое расстояние было между автомобилями в 7 ч того же дня, если скорость легкового автомобиля 66 км/ч? Есть ли в условии лишние (избыточные) данные?
№ 1.26. Фотовыставка размещена в сквере на стендах. Стенды расставлены вокруг квадратного газона со стороной 46 м. Посетители рассматривают экспозицию, двигаясь со скоростью 0,016 м/с. Смогут ли они за час обойти всю выставку?
№ 1.27. Заполните таблицу.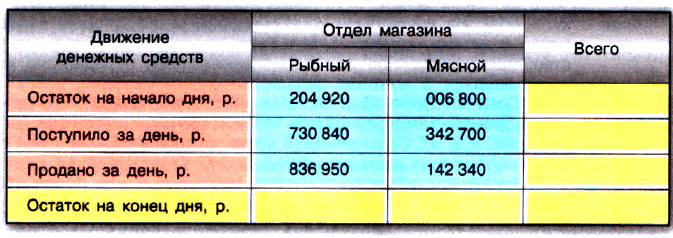
№ 1.28. Найдите значение выражения: 1) (59 – 26,42) • 3,5; 2) (9 – 4,58) • 0,5.
№ 1.29. Найдите среднее арифметическое чисел:
а) 43,25; 41,64; 38,24; 47,82 и округлите ответ до десятых;
б) 7,126; 5,364; 3,275; 1,932 и округлите ответ до тысячных.
№ 1.30. Найдите среднюю длину своего шага, измерив длину пяти своих шагов.
№ 1.31. Три поля имеют площадь по 100 га каждое. С первого поля собрали 3610 ц пшеницы, со второго — 3780 ц пшеницы, с третьего — 3545 ц пшеницы. Определите урожайность пшеницы на каждом поле и найдите среднюю урожайность на трёх полях.
№ 1.32. Велосипедист ехал 2,6 ч со скоростью 6,6 м/с, а затем 1,4 ч со скоростью 5,2 м/с. Чему равна средняя скорость движения велосипедиста на всём пути?
№ 1.33. Одно число равно 5,9. Найдите другое число, если среднее арифметическое двух чисел 3,2.
№ 1.34. Среднее арифметическое двух чисел 4,9. Одно из них в 1,8 раза меньше другого. Найдите эти числа.
№ 1.35. Среднее арифметическое двух чисел 5. Найдите эти числа, если первое число на 2,5 больше второго.
№ 1.36. За 7 ч комбайнёр убрал кукурузу с 9,8 га поля. С какой скоростью двигался комбайн, если ширина жатки равна 3,5 м?
№ 1.37. На одну порцию десерта из клубники берут 120 г ягод и 25 г сливок. Сколько килограммов сливок потребуется для приготовления десерта из 24 кг клубники? Сколько порций получится?
№ 1.38. Биомасса — это шестой по запасам из источников энергии на Земле после горючих сланцев, урана, угля, нефти и природного газа. Ежегодно на Земле образуется около 170 млрд т первичной биологической массы. Биомасса растительности лугов, степей и пашен составляет около 70 % от первичной биомассы. Найдите, сколько баррелей нефти она может заменить, если 380 т дают столько же энергии, сколько один баррель нефти. Ответ округлите до целого числа миллионов.
№ 1.39. Найдите значение выражения:
а) 4,3x + 6,9x + 7,7x – 5,9x при x = 5,4; 0,6; 100;
б) 4,9а – (3,9а + 0,6а) при а = 3,2; 9,38;
в) 19,84с – (7,84с + 11,7с) при с = 0,4; 5,02.
№ 1.40. Вычислите: а) 42,885 – 27,885 : (0,72 + 4,35); б) 241,18 + 258,82 : (39 – 36,5).

ПРОВЕРЬТЕ СЕБЯ
Проверочная работа
- Найдите среднее арифметическое чисел:
а) 5, 4, 1, 0, 9, 3, 1, 0, 0, 5;
б) 10, 34, 65, 48, 96;
в) 4,9; 5,1; 5; 4,8; 5,2;
г) 20,1; 100,6; 21; 20,5; 105,8. - Одно число равно 6,4. Чему равно другое число, если среднее арифметическое этих двух чисел равно 3,25?
- Среднее арифметическое двух чисел равно 146. Найдите эти числа, если одно число больше другого на 22.
- Велосипедист ехал 6 мин в гору, преодолев 1,2 км, затем он проехал 5,3 км по велосипедной дорожке, затратив на этот участок дороги 12 мин. По лесной тропинке протяжённостью 2,3 км он ехал 15 мин. С какой средней скоростью ехал велосипедист? Ответ запишите в км/ч.
- * а) Среднее арифметическое трёх последовательных натуральных чисел равно 21. Найдите эти три числа.
б) Сформулируйте правило для нахождения среднего арифметического трёх последовательных натуральных чисел.
<< §6 п.44 Вернуться в ОГЛАВЛЕНИЕ §1 п.2 >>
Вы смотрели: Математика Виленкин Учебник 1 «Среднее арифметическое» (задания 1.1 — 1.40) из § 1 «ВЫЧИСЛЕНИЯ И ПОСТРОЕНИЯ». Ознакомительный фрагмент учебника 2023 года.