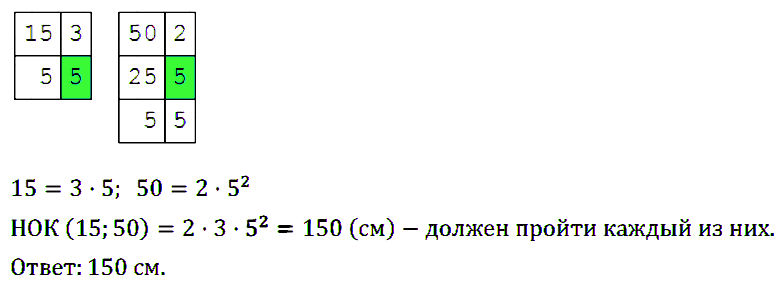Упражнения по математике для УМК Мерзляк с ответами на некоторые задачи. §6. Наименьшее общее кратное (2019, 2020, 2021 годы). Математика 6 Мерзляк. Упражнения 163-186.
ОГЛАВЛЕНИЕ (2021 год) ТЕОРИЯ: § 6.
Математика 6 Мерзляк (2021 год)
§ 6. Упражнения 163-186
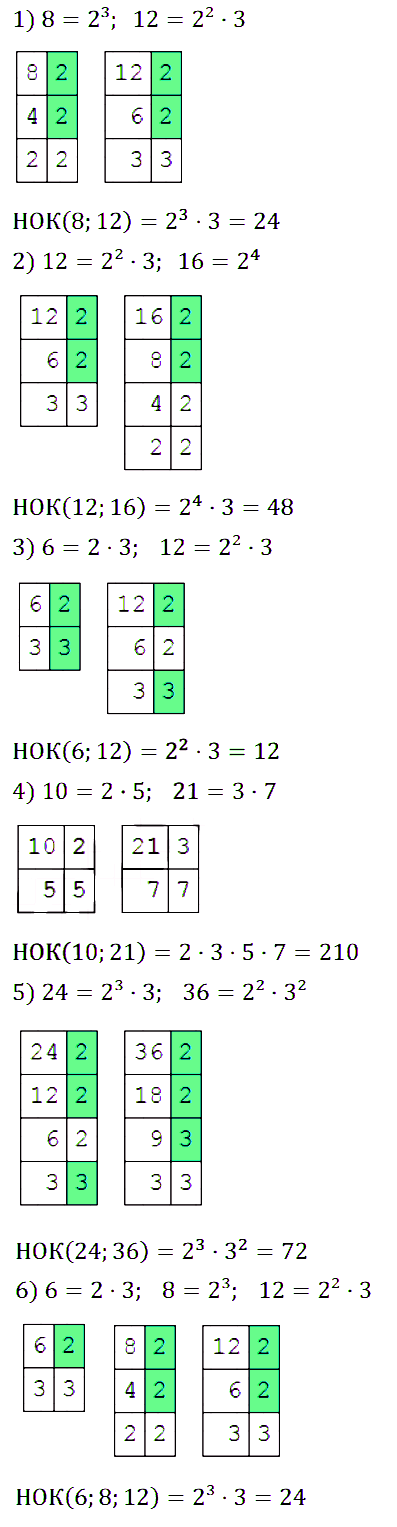
№ 163. Найдите наименьшее общее кратное чисел: 1) 8 и 12; 2) 12 и 16; 3) 6 и 12; 4) 10 и 21; 5) 24 и 36; 6) 6, 8 и 12.
Правильный ответ: 1) НОК (8; 12) = 23 • 3 = 24; 2) НОК (12; 16) = 24 • 3 = 48; 3) НОК (6; 12) = 22 • 3 = 12; 4) НОК (10; 21) = 2 • 3 • 5 • 7 = 210; 5) НОК (24; 36) = 23 • 32 = 72; 6) НОК (6; 8; 12) = 23 • 3 = 24.
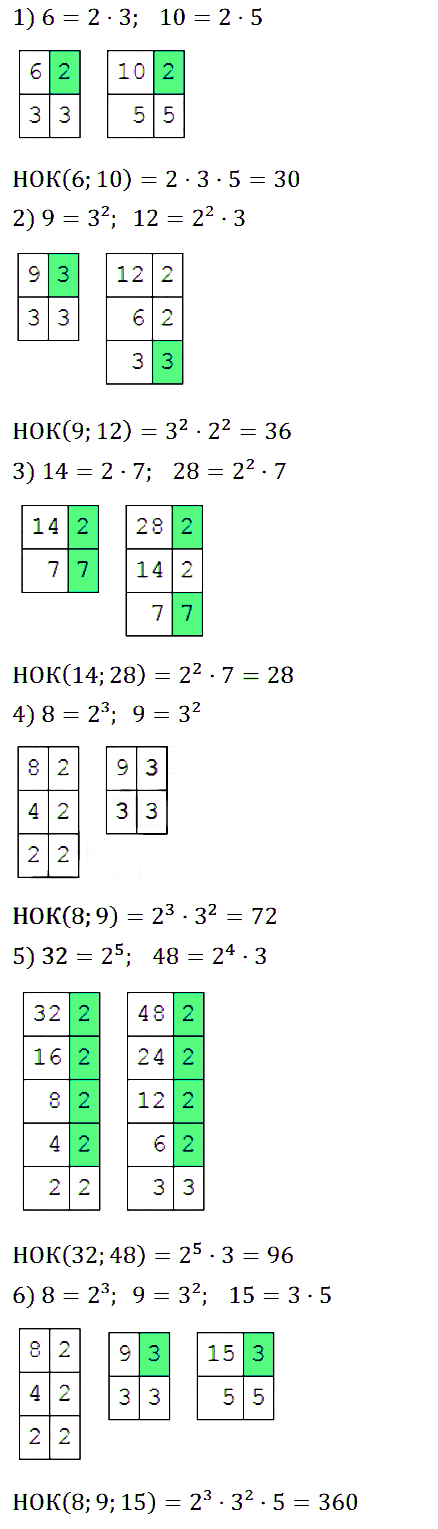
№ 164. Найдите наименьшее общее кратное чисел: 1) 6 и 10; 2) 9 и 12; 3) 14 и 28; 4) 8 и 9; 5) 32 и 48; 6) 8, 9 и 15.
Правильный ответ: 1) HOK (6; 10) =2 • 3 • 5 = 30; 2) НОК (9; 12) = 32 • 22 = 36; 3) НОК (14; 28) = 22 • 7 = 28; 4) Н0К (8; 9) = 23 • 32 = 72; 5) НОК (32; 48) = 25 • 3 = 96; 6) НОК (8; 9; 15) = 23 • 32 • 5 = 360.
№ 165. Найдите наибольший общий делитель и наименьшее общее кратное чисел а и b: 1) а = 23 • 3 • 5 и b = 2 • 32 • 5; 2) а = 24 • 3 • 11 и b = 22 • 33 • 13.
Правильный ответ: 1) Если а = 23 • 3 • 5; b = 2 • 32 • 5, то НОД (а; b) = 2 • 3 • 5 = 30; НОК (а; b) = 23 • 32 • 5 = 360.
2) Если а = 24 • 3 • 11; b = 22 • 33 • 13, то НОД (а; b) = 22 • 3 = 12; НОК (а; b) = 24 • 33 • 11 • 13 = 61 776.
№ 166. Найдите наибольший общий делитель и наименьшее общее кратное чисел а и b: 1) a = 3 • 52 и b = 3 • 5 • 7; 2) а = 23 • З2 • 54 и b = 22 • 33 • 52.
Правильный ответ: 1) Если а = 3 • 52; b = 3 • 5 • 7, то НОД (а; b) = 3 • 5 = 15; НОК (а; b) = 3 • 52 • 7 = 525.
2) Если а = 23 • 32 • 54; b = 22 • 33 • 52, то НОД (а; b) = 22 • 32 • 52 = 900; НОК (а; b) = 23 • 33 • 54 = 135 000.
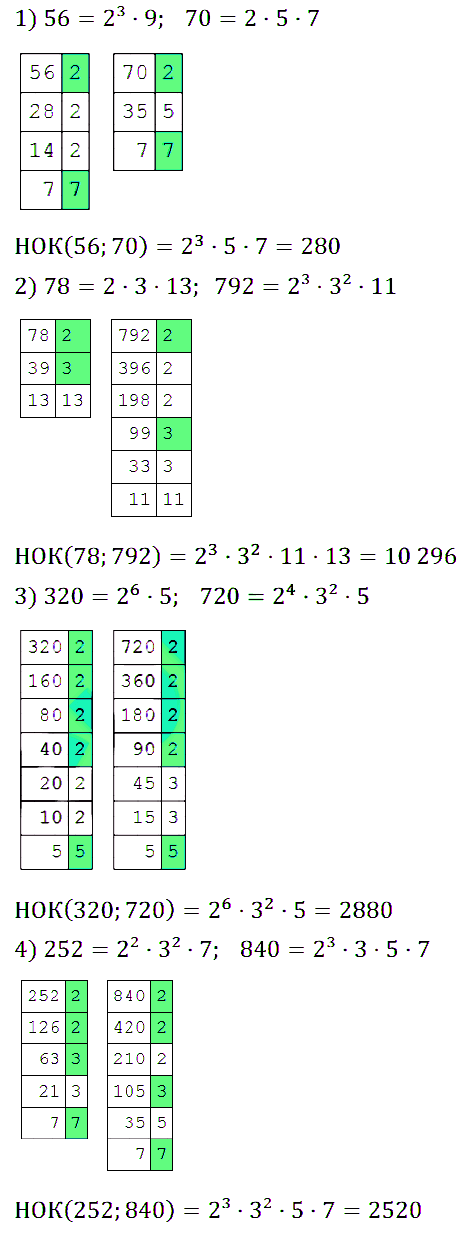
№ 167. Найдите наименьшее общее кратное чисел: 1) 56 и 70; 2) 78 и 792; 3) 320 и 720; 4) 252 и 840.
Правильный ответ: 1) НОК (56; 70) = 23 • 5 • 7 = 280; 2) НОК (78; 792) = 23 • 32 • 11 • 13 = 10 296; 3) НОК (320; 720) = 26 • 32 • 5 = 2880; 4) НОК (252; 840) = 23 • 32 • 5 • 7.
№ 168. Найдите наименьшее общее кратное чисел: 1) 42 и 63; 2) 120 и 324; 3) 675 и 945; 4) 924 и 396.
Правильный ответ: 1) НОК (42; 63) = 2 • 32 • 7 = 126; 2) НОК (120; 324) = 23 • 34 • 5 = 3240; 3) НОК (675; 945) = 33 • 52 • 7 = 4725; 4) НОК (924; 396) = 22 • 32 • 7 • 11 = 2772.
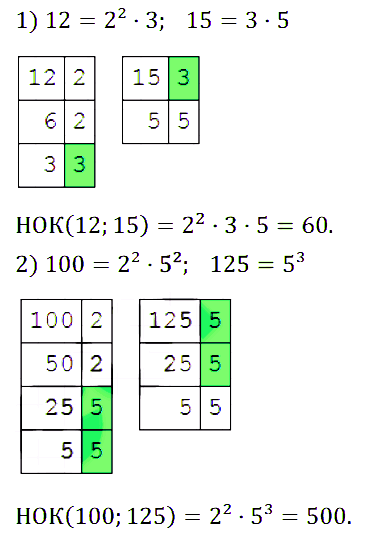
№ 169. Найдите наименьшее общее кратное знаменателей дробей: 1) 11/12 и 4/15; 2) 97/100 и 1/125.
Правильный ответ: 1) НОК (12; 15) = 22 • 3 • 5 = 60. 2) НОК (100; 125) = 22 • 53 = 500.
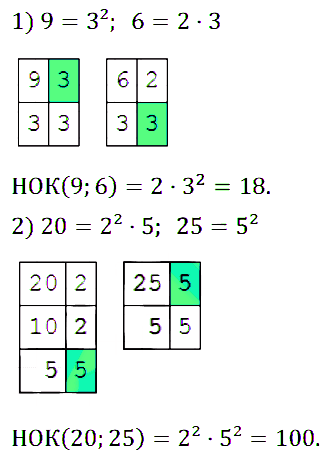
№ 170. Найдите наименьшее общее кратное знаменателей дробей: 1) 8/9 и 7/6; 2) 11/20 и 24/25.
Правильный ответ: 1) НОК (9; 6) = 2 • 32 = 18. 2) НОК (20; 25) = 22 • 52 = 100.
№ 171. Найдите наименьшее общее кратное: 1) первых пяти натуральных чисел; 2) первых пяти нечётных чисел; 3) первых пяти простых чисел.
Правильный ответ: 1) НОК (1; 2; 3; 4; 5) = 1 • 22 • 3 • 5 = 60.
2) НОК (1; 3; 5; 7; 9) = 1 • 32 • 5 • 7 = 315.
3) НОК (2; 3; 5; 7; 11) = 2 • 3 • 5 • 7 • 11 = 2310.
№ 172. Найдите наименьшее общее кратное: 1) первых пяти чётных чисел; 2) первых четырёх составных чисел.
Правильный ответ: 1) НОК (2; 4; 6; 8; 10) = 23 • 3 • 5 = 120.
4 = 22; 6 = 2 • 3; 8 = 23; 10 = 2 • 5.
2) НОК (4; 6; 8; 9) = 23 • 32 = 72.
4 = 22; 6 = 2 • 3; 8 = 23; 9 = 32.
№ 173. Длина шага Чебурашки равна 15 см, а крокодила Гены – 50 см. Какое наименьшее одинаковое расстояние должен пройти каждый из них, чтобы они оба сделали по целому числу шагов?
Правильный ответ: 150 см.
№ 174. С одного места в одном направлении по велотреку одновременно стартовали два велосипедиста. Один из них делает крут за 1 мин, а другой – за 45 с. Через какое наименьшее количество минул’ после начала движения они вновь окажутся в месте старта? Сколько кругов по велотреку при этом сделает каждый из них?
Правильный ответ: 3 минуты; 3 круга; 4 круга.
№ 175. Дима и Петя отправились в поход из одного пункта в одном направлении. Петя делал остановку для отдыха через каждые 2 400 м, а Дима – через каждые 2 800 м. На каком наименьшем расстоянии от пункта отправления места их остановок совпадут?
Правильный ответ: 16 800 м.
№ 176. В ящике лежит меньше 80 мандаринов. Известно, что их можно разделить поровну между двумя, тремя или пятью детьми, но нельзя разделить поровну между четырьмя детьми. Сколько мандаринов лежит в ящике?
Правильный ответ: 30 мандаринов.
Решение: Число мандаринов должно делиться на 2, 3, и 5 и не делиться на 4. => НОК (2; 3; 5) = 2 • 3 • 5 = 30 (мандаринов) – лежит в ящике.
№ 177. Саша ходит в бассейн один раз в три дня, Коля – раз в четыре дня, Петя – раз в пять дней. Мальчики встретились в бассейне во вторник. Через сколько дней и в какой день недели они встретятся в следующий раз?
Правильный ответ: через 60 дней, в субботу.
Решение: НОК (3; 4; 5) = 3 • 4 • 5 = 60 дней.
вторник + 60 дней = вторник + 8 педель + 4 дня => вторник + 4 дня = суббота.
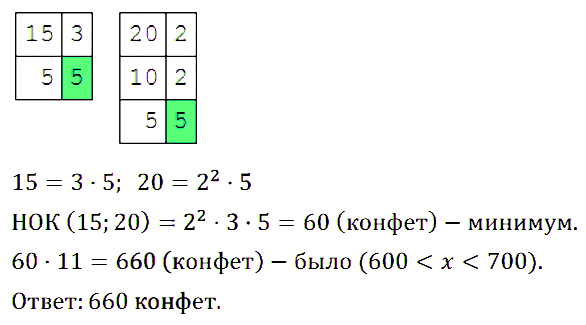
№ 178. Готовя подарки к Новому году, члены родительского комитета 6 класса увидели, что имеющиеся конфеты можно разложить поровну по 15 штук или по 20 штук в один подарок. Сколько было конфет, если известно, что их было больше 600 и меньше 700?
Правильный ответ: 660 конфет.
№ 179. Если к данному числу прибавить 2, то полученное число будет кратно 5. Чему равен остаток от деления данного числа на 5?
Правильный ответ: 5 – 2 = 3 (остаток).
№ 180. Белый аист пролетел 48 км со скоростью 40 км/ч. Сколько взмахов крыльями сделал мри этом аист, если каждую секунду он делает два взмаха?
Правильный ответ: 8640 взмахов.
48 : 40 = 1,2 ч = 72 мин = 4320 с.
4320 • 2 = 8640 (взмахов) – сделал при этом аист.
№ 181. Для производства 1 т бумаги необходимо использовать 6,3 м3 древесины или 1400 кг макулатуры. Учащиеся одной школы собрали 2100 кг макулатуры. Сколько кубических метров древесины можно сэкономить, использовав для производства бумаги собранную школьниками макулатуру?
Правильный ответ: 9,45 м3.
Решение: 1) 2100 : 1400 = 21 : 14 = 1,5 (раза) – больше бумаги можно получить из 2100 кг макулатуры, чем из 1400 т.
1 • 1,5 = 1,5 (тонны) – бумаги из 2100 кг макулатуры.
2) 6,3 • 1,5 = 9,45 (м3) – древесины можно сэкономить.
№ 182. Останкинская телебашня в Москве является самой высокой в Европе отдельно стоящей конструкцией. Высота Эйфелевой башни (г. Париж, Франция) вместе с антенной равна 324 м, что составляет 3/5 высоты Останкинской телебашни. Останкинская телебашня состоит из железобетонной основы и металлической части, которая короче железобетонной основы на 230 м. Какова высота железобетонной основы?
Правильный ответ: 385 м.
Решение: 1 способ. 1) 324 : 3 • 5 = 108 • 5 = 540 (м) – высота Останкинской телебашни.
2) Пусть х м – металлическая часть башни, тогда (х + 230) м – железобетонная основа. Мы нашли, что высота всей башни 540 м. Составим уравнение: х + х + 230 = 540 ==> 2х = 540 – 230
2х = 310 ==> х = 155 (м) – металлическая часть.
155 + 230 = 385 (м) – железобетонная основа Останкинской телебашни.
2 способ. 1) 324 : 3 • 5 = 108 • 5 = 540 (м) – высота Останкинской телебашни.
2) 540 + 230 = 770 (м) – удвоенная высота железобетонной основы.
3) 770 : 2 = 385 (м) – высота железобетонной основы.
№ 183. 1) В коробке лежит 14 шаров, из которых 5 – синего цвета. Какую часть всех шаров составляют синие?
Правильный ответ: 5/14 часть.
№ 183. 2) В коробке лежит 14 шаров, из которых составляют шары красного цвета. Сколько красных шаров в коробке?
Правильный ответ: 6 красных шаров (14 : 7 • 3 = 6 (шаров) – в коробке красные).
№ 183. 3) В коробке лежат шары, 6 из которых белого цвета. Сколько всего шаров в коробке, если белые составляют 3/7 всех шаров?
Правильный ответ: 14 шаров (6 • 7 : 3 = 42 : 3 = 14 (шаров) – всего в коробке. ).
№ 184. Укажите, какие из дробей 12/17, 12/7, 5/13, 15/13, 374/10, 53/8, 53/54, 72/71: 1) правильные; 2) неправильные. Неправильные дроби преобразуйте в смешанные числа.
Правильный ответ: 1) Правильные дроби: 12/17; 5/13; 53/54.
2) Неправильные дроби: 12/7; 15/13; 374/10; 53/8; 72/71.
Преобразование в смешанные дроби: 12/7 = 1 5/7; 15/13 = 1 2/13; 374/10 = 37 4/10; 53/8 = 6 5/8; 72/71 = 1 1/71.
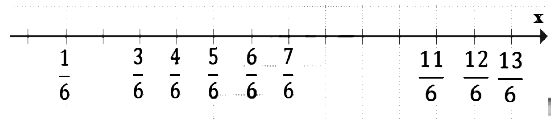
№ 185. Начертите координатный луч, взяв за единичный такой отрезок, длина которого в 6 раз больше стороны клетки тетради. Отметьте на луче точки, соответствующие числам: 1/6, 3/6, 4/6, 5/6, 6/6, 7/6, 11/6, 12,/6, 13/6.
№ 186. На чудо-дереве садовник вырастил 85 бананов и 70 апельсинов. Каждый день он срывает два плода, и сразу на дереве вырастает один новый. Если садовник срывает два одинаковых фрукта, то вырастает апельсин, а если два разных – то банан. Каким окажется последний фрукт на этом дереве?
Правильный ответ: останется банан.
Решение: 1) Срывает 2 апельсина вырос апельсин, количество бананов не изменилось.
2) Срывает 2 банана вырос апельсин, бананов нечетное число (уменьшилось на 2).
3) Срывает апельсин + банан => вырос банан, количество бананов не изменилось.
Количество бананов всегда остается нечетным, значит их не может быть 0.
ОГЛАВЛЕНИЕ (2021 год) ДАЛЕЕ: Упражнения 187-209
Вы смотрели: Упражнения по математике для УМК Мерзляк с ответами на некоторые задачи. §6. Наименьшее общее кратное (2019, 2020, 2021 годы). Математика 6 Мерзляк. Упражнения 163-186. ГДЗ по новому учебнику (Решебник упражнений).