Контрольная работа по математике в 6 классе № 1 «Делимость натуральных чисел» (Методическое пособие, варианты 1-2 из 4-х), а также решения и ОТВЕТЫ на нее (нет в пособии). Код материалов: Математика Мерзляк КР01 В12 МП6.
Другие варианты: К-1 Варианты 1-2 ДМ К-1 Варианты 3-4 МП
Вернуться к Списку контрольных работ (в ОГЛАВЛЕНИЕ)
Математика 6 класс (УМК Мерзляк). Методическое пособие (Буцко и др.)
Контрольная № 1. Вариант № 1
№ 1. Из чисел 387, 756, 829, 2 148 выпишите те, которые делятся нацело: 1) на 2; 2) на 9.
ОТВЕТ: 1) 756; 2148. 2) 387; 756.
№ 2. Разложите число 756 на простые множители.
ОТВЕТ:
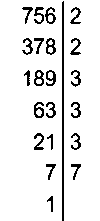
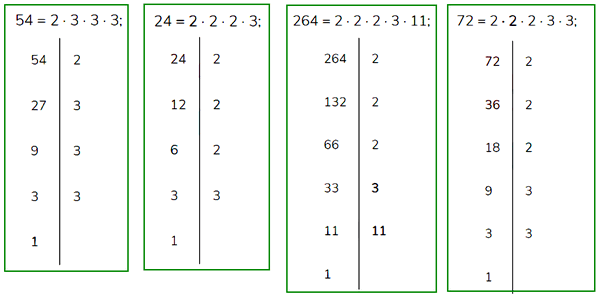
№ 3. Найдите наибольший общий делитель чисел: 1) 24 и 54; 2) 72 и 264.
ОТВЕТ: 1) НОД (24; 54) = 2 • 3 = 6. 2) НОД (72; 264) = 2 • 2 • 2 • 3 = 24.
№ 4. Найдите наименьшее общее кратное чисел: 1) 16 и 32; 2) 15 и 8; 3) 16 и 12.
ОТВЕТ: 1) НОК (16; 32) = 32. 2) НОК (15; 8) = 15 • 8 = 120. 3) НОК (16; 12) = 4 • 4 • 3 = 48.
№ 5. Докажите, что числа 272 и 1 365 – взаимно простые.
Доказательство: Взаимно простые числа — целые числа, не имеющие никаких общих делителей, кроме 1.

1365 = 3 • 5 • 7 • 13; 272 = 2 • 2 • 2 • 2 • 17.
272 и 1 365 имеют только одни общий делитель, равный 1. Что и требовалось доказать.
№ 6. Вместо звёздочки в записи 1 52* поставьте цифру так, чтобы полученное число было кратным 3 (рассмотрите все возможные случаи).
Решение: 1 + 5 + 2 = 9
9+0=9, кратно 3; 9+3=12, кратно 3; 9+6=15, кратно 3; 9+9=18, кратно 3.
ОТВЕТ: * = 0; 3; 6; 9.
№ 7. Петя расставил книги поровну на 12 полках, а потом переставил их, тоже поровну, на 8 полок. Сколько книг было у Пети, если известно, что их было больше 100, но меньше 140?
Решение: Число книг должно быть кратно:
НОК (12; 8) = 4 • 3 • 2 = 24.
100 : 24 = 4 (ост. 4)
100 < 24 • 5 < 140
100 < 120 < 140.
Значит, у Пети было 120 книг (24 • 5)
ОТВЕТ: 120 книг.
Контрольная № 1. Вариант № 2
№ 1. Из чисел 405, 972, 865, 2 394 выпишите те, которые делятся нацело: 1) на 5; 2) на 9.
ОТВЕТ: 1) 405, 865; 2) 405, 972, 2394.
№ 2. Разложите число 1 176 на простые множители.
ОТВЕТ:
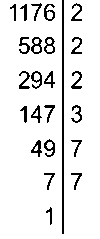
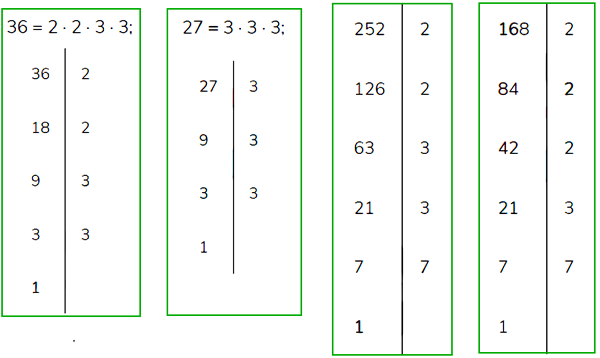
№ 3. Найдите наибольший общий делитель чисел: 1) 27 и 36; 2) 168 и 252.
ОТВЕТ: 1) НОД (27; 36) = 3 • 3 = 9 (36 = 2 • 2 • 3 • 3; 27 = 3 • 3 • 3);
2) НОД (168; 252) = 2 • 2 • 3 • 7 = 84.
№ 4. Найдите наименьшее общее кратное чисел: 1) 11 и 33; 2) 9 и 10; 3) 18 и 12.
ОТВЕТ: 1) НОК (11; 33) = 33.
2) НОК (9; 10) = 9 • 10 = 90.
3) НОК (18; 12) = 6 • 3 • 2 = 36.
№ 5. Докажите, что числа 297 и 304 – взаимно простые.
Доказательство: Взаимно простые числа — целые числа, не имеющие никаких общих делителей, кроме 1.

297 и 304 имеют только один общий делитель, равный 1, так как 304 = 2 • 2 • 2 • 2 • 19; 297 = 3 • 3 • 3 • 11.
№ 6. Вместо звёздочки в записи 1 99* поставьте цифру так, чтобы полученное число было кратным 3 (рассмотрите все возможные случаи).
Решение: 1 + 9 + 9 = 19.
19+2=21, кратно 3; 19+5=24, кратно 3; 19+8=27, кратно 3.
ОТВЕТ: * = 2; 5; 8.
№ 7. Собранный урожай яблок фермер может разложить поровну в корзины по 12 кг или в ящики по 15 кг. Сколько килограммов яблок собрал фермер, если известно, что их было больше 150 кг, но меньше 200 кг?
Решение: Масса яблок должна быть кратна:
НОК (12; 15) = 4 • 3 • 5 = 60.
150 : 60 = 2 (ост. 30)
150 < 3 • 60 < 200
150 < 180 < 200. Значит, фермер собрал 180 кг яблок.
ОТВЕТ: 180 кг.
Вы смотрели: Математика Мерзляк КР01 В12 МП6 — Контрольная работа № 1 по математике в 6 классе по теме «Делимость натуральных чисел» (варианты 1-2 МП): задания, решения и ответы на нее.
Другие варианты: К-1 Варианты 1-2 ДМ К-1 Варианты 3-4 МП
Вернуться к Списку контрольных работ (в ОГЛАВЛЕНИЕ)